Post-scriptum : Le titre « Aire de figures simples ». Quatre minutes et quinze secondes d’animation (*). L’idée était audacieuse et passionnante. « L’animation » provenait des figures simples elles-mêmes : en se présentant et en se représentant comme de véritables « personnages », elles nous incitaient à comparer et distinguer…

« Le rond », le disque, en posant et composant le point initiait et marquait cette mise en scène. Il était à la fois le point « sur le I » et le point « final » d’une première phrase, une première séquence de trois secondes. Ce « gonflement-pulsation » était une trouvaille et une annonce…

Les figures s’arrachaient à la surface plane, l’une après l’autre, de la gauche vers la droite, Elles semblaient ainsi « faire place » mais aussi déclencher une autre pulsation, vite interrompue et comme stabilisée par (sur) l’horizontale : La ligne d’écriture s’annonçait, installait son importance.

La métaphore était belle : le savoir comme un nuage, difficile à voir, à saisir parce que trop diffus, trop dispersé. La réalisation, la mise en scène était soignée : le tableau noir, la craie, la poussière de la craie qui peu à peu se rassemble, s’installe, se fixe…

La mise en scène du carré/unité de mesure, l’explosion (ci-dessus)du nuage de poussière de craie initiant les dix secondes d'animation avaient, elles aussi, un sens métaphorique. Le carré original, mémorisé (le savoir), échappait à l’explosion, se déformait, se transformait en un rectangle.

Carré ou rectangle, l'un comme l'autre, permettait de disposer...

... et de comptabiliser facilement les unités de mesure. Le problème posé était celui du langage. Au niveau des mathématiques « élémentaires », il était souvent ignoré. Ce qui était montré était simple à comprendre : ce qui était dit (dessiné ou écrit) se lisait et « s’interprétait » facilement...

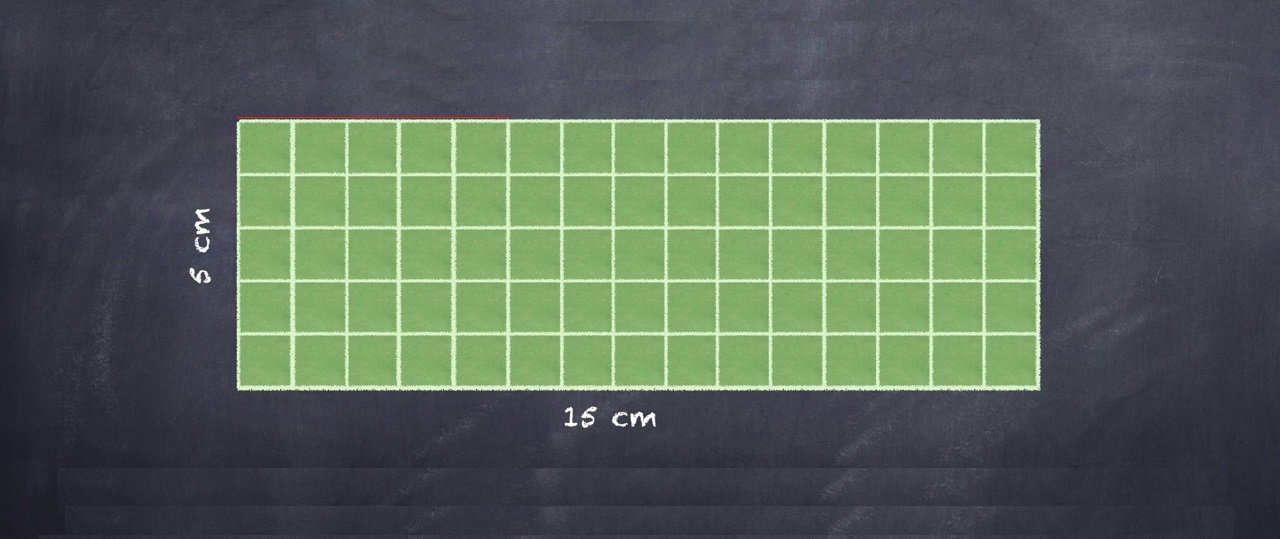
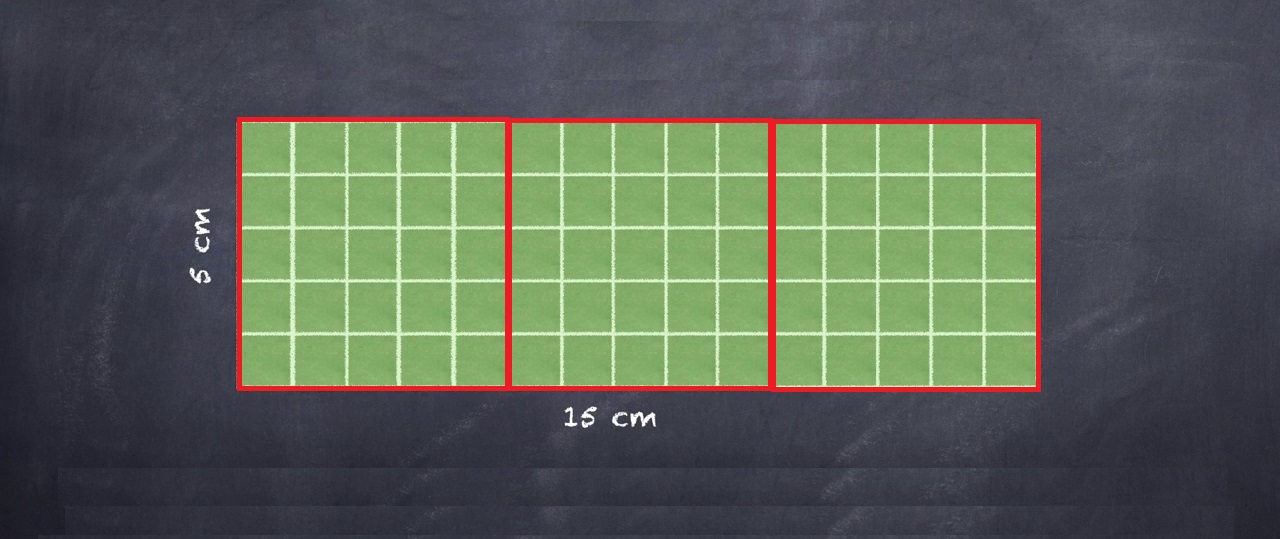
« Les paroles s’envolent, les écrits restent »… l’adage est bien connu. Les mathématiques sont un langage écrit, soumis à « l’arrêt sur image » comme ci-dessus à droite ce « 5 × 15 = 75 cm² ».

Aucun d’entre nous n’écrira que « 75 = 75 cm² ».

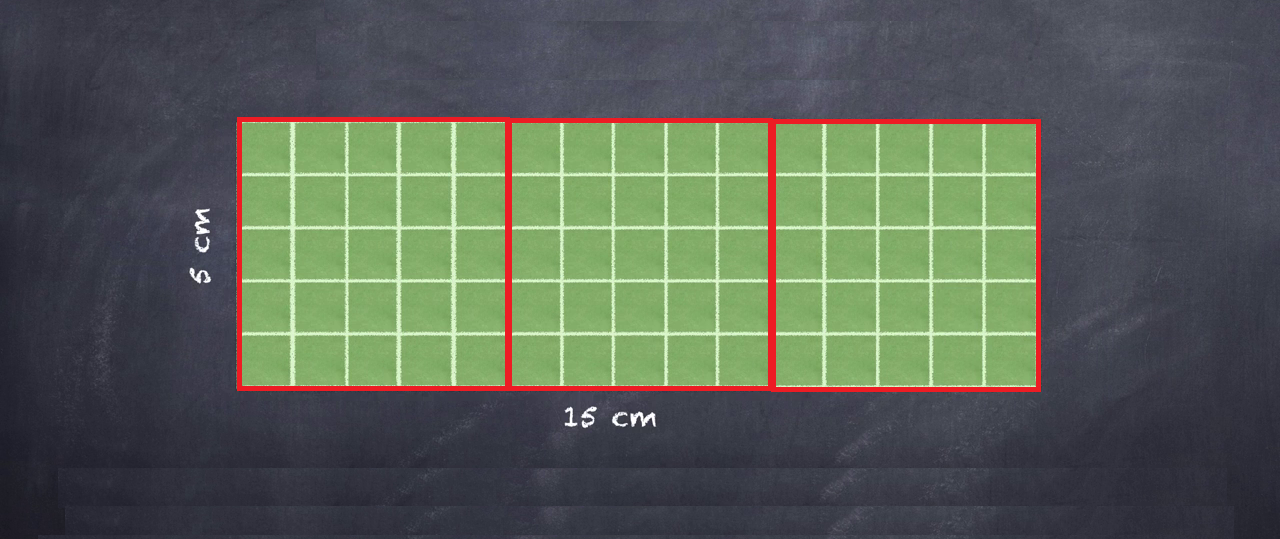
En langage courant, usuel : « 75 » et « 75 cm² », c’est pas pareil, c’est pas la même « chose ». L’égalité est un élément de langage essentiel en (aux) mathématique(s).

Qui se souciait de remarquer ces 5 cm sur 15 cm ? Quel grammairien serait assez sévère pour corriger la conclusion ci-dessus. Chacun d'entre nous, grammairien ou pas, conviendra pourtant que la phrase :
    « On peut ranger 15 colonnes de 5 carrés de 1 cm² »  se traduit naturellement par :

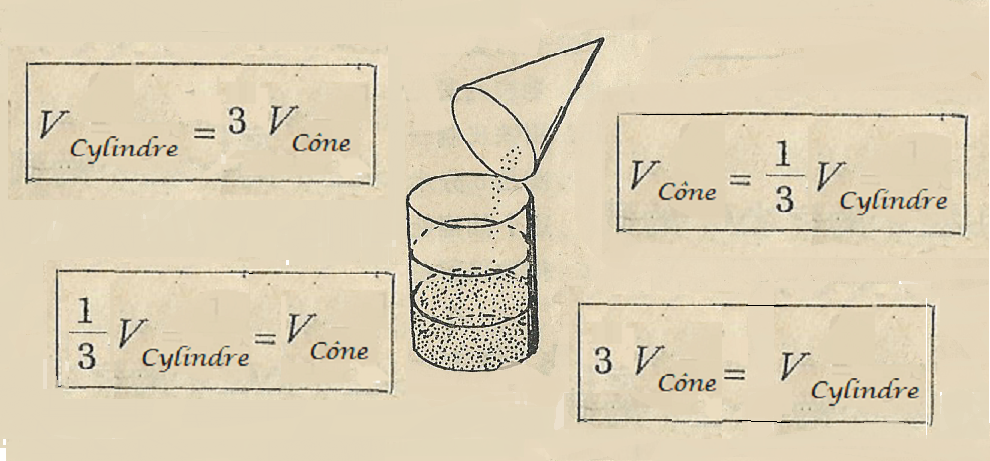
Trois fois plus... grand mais aussi  —  et en même temps —  trois fois moins.... Depuis des milliers d'année, cette expresion avait un sens. Depuis des milliers d'années, elle donnait forme au calcul des grandeurs.