
Nombres, Grandeurs, Vecteurs
Les deux logiciels ci-dessous mettent en scène deux grandeurs : l'«Aire» (Aires de figures simples) et le «Volume» (Volume de solides usuels). Aucun son, aucun commentaire, aucun « accompagnement » musical. La mise en scène est celle du tableau noir scolaire et de nuages de craie d’où surgissent tout à coup des figures ou des lettres qui se rassemblent en phrases (*)…
Je dois beaucoup à la créativité et à l’inventivité de l'auteur (des auteurs ?) de ces animations. A l'image de Rythmétic et entre autres « copiés/volés/empruntés » (*), cette mise en scène de la dizaine…

Le réel, la réalité, le jeu de cubes (*), image, imagination, langage, entremélés, entremèlant...





... cinq objets mathématiques : nombre, longueur, aire, volume, vecteur… la mesure des grandeurs et la numération décimale constituées en complexe d'apprentissage par une simple question...
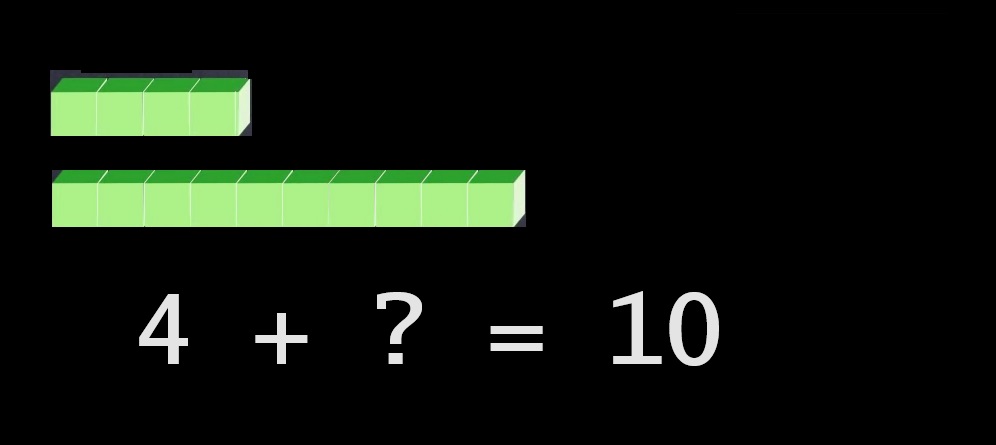
... combien doit-on ajouter à « 4 » pour constituer une dizaine ?
Imaginons un logiciel, reproduisant comme ci-dessus cette demande et, face à cet écran, plaçons un jeune enfant : il a passé et dépassé l'âge heureux des comptines, l'âge où il chantait un, deux trois, nous irons au bois. Il a découvert et appris à réciter sur « ses » doigts, les mots qu'il va associer à « ses » premiers nombres. Face à cet écran, aura-t-il beaucoup de mal à bien répondre ? Je pense que non.
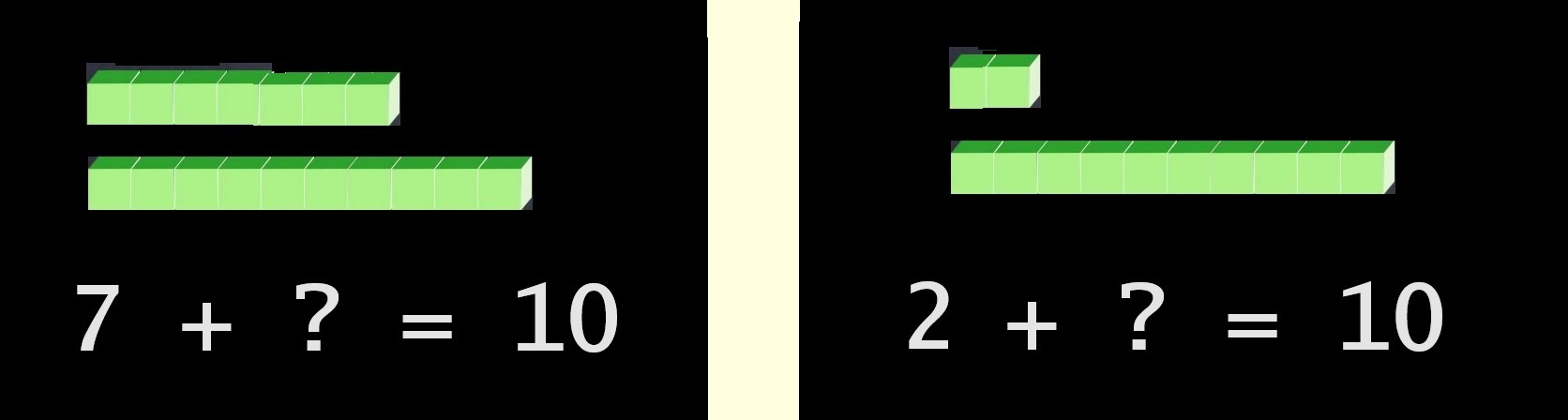
Le logiciel que nous imaginons n'en pense rien mais se doit de tout prévoir... Chaque bonne réponse sera donc, si l'on peut dire, « sanctionnée » par l'apparition d'une nouvelle question :
En cas d'erreur, c'est-à-dire d'un autre appui que celui effectué sur la « bonne » touche du pavé numérique, apparaitra une aide comme ci-dessous (mauvaise réponse à la question : 4 + ? = 10) :
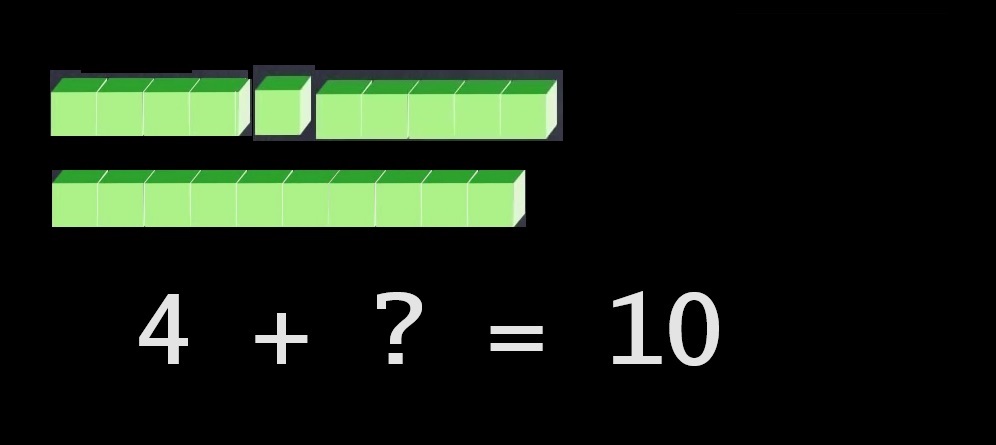
L'enfant recherche et frappe la « bonne » touche sur son clavier numérique : réponse immédiate...
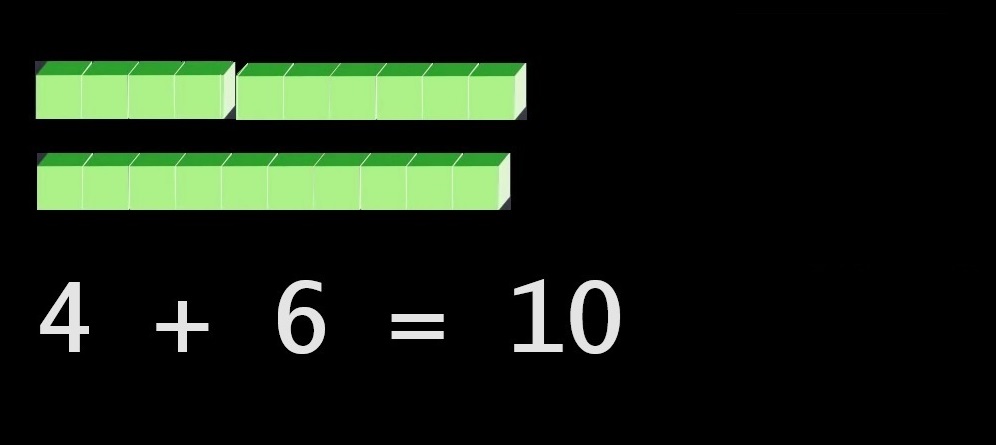
... quelques secondes... un nouvel écran, de nouvelles questions :
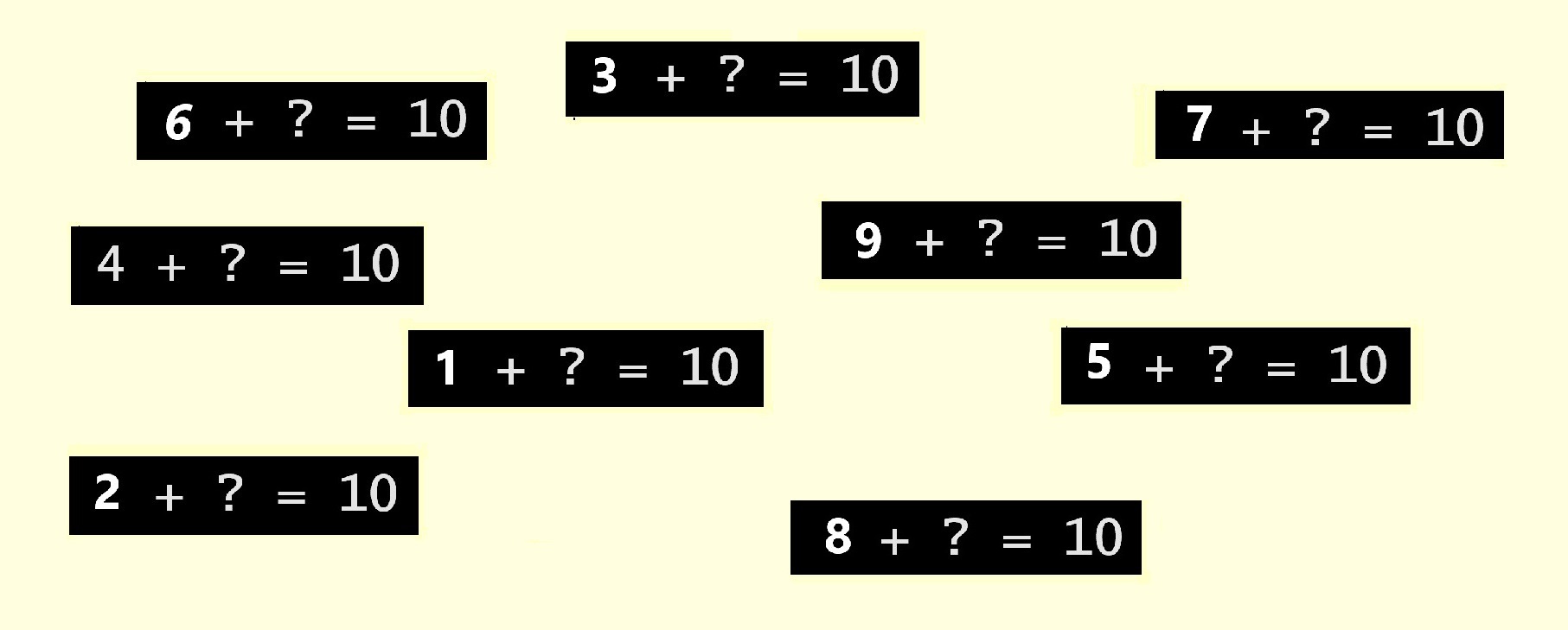
Une cinquantaine de questions, choisies, produites et reproduites de façon aléatoire, chaque « bonne » réponse étant marquée de l'apparition d'une nouvelle question (*). Les premières « frappes » étaient « réfléchies », mais la répétition des mêmes questions entraine la mémorisation de leur réponse et l’exercice devient « facile » : la réponse « surgit » d’elle-même dans le cerveau de l’enfant et il n’a plus qu’à la « transformer » en une « frappe », le choix d’une touche de son pavé numérique.
L'interruption de l'exercice est brutale : une annonce, des félicitations, une proposition...

L’exercice est oublié ; c’est un défi qui est proposé à l’élève, à l’enfant : face à l’immédiateté des réactions de « l’ordinateur », la rapidité de ses réponses est en jeu. Il appuie sur la touche « O ».
. . .
Ces apprentissages sont ceux d’un automatisme. Ils n’ont d’importance que parce qu'ils utilisent « l’égalité » mathématique. Ils permettent à notre jeune élève d’accéder à un savoir qui est et sera d’abord un savoir-faire. La grammaire d’un langage s’apprend avant tout par l’usage et à ce niveau élémentaire, elle n’est pas étudiée ni même évoquée. Notre élève imaginaire est un écolier ou un collégien, un usager de l’institution scolaire : il en a le langage, les savoirs et savoir-faire. Plaçons-le face aux deux égalités…
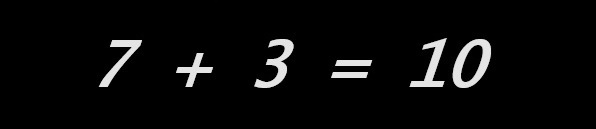
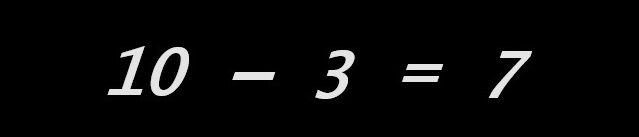
… ci-dessus et interrogeons-le : connait-il, reconnait-il ce qui est écrit ? Notre élève vous répondra en vous précisant qu’il reconnait, à gauche une addition et à droite une soustraction. Remarquons ici que nous sommes vous et moi d’anciens élèves et que nous serons nombreux à répondre comme lui.