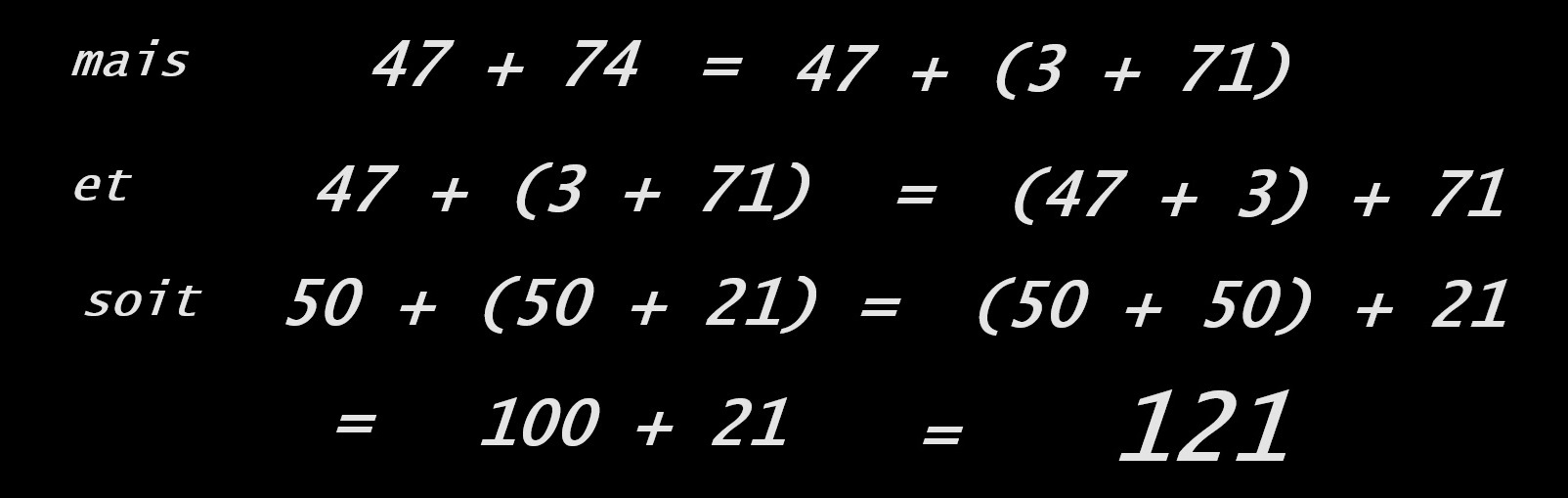
La logique de l'écriture
Le langage : « As-tu fait tes opérations ? ». La réalité : quelques lignes de son cahier d’exercices.
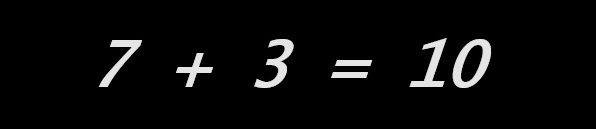
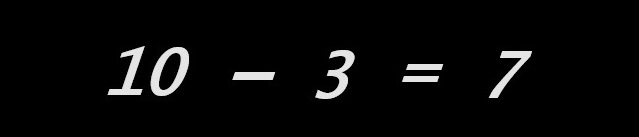
L'imagination : consciemment ou non, notre élève accorde une attention particulière au côté droit de l’égalité. Pour lui ce côté droit est celui de la (de sa) réponse. Il est réduit au seul nombre-résultat. Ce privilège sera encore renforcé lorsque notre élève apprendra à résoudre « ses » premières équations, ses premiers « calculs en x ». Ce travail se fait sur plusieurs lignes d'égalités disposées en regard, mais ne se juge que sur la dernière, celle de la « réponse », qui se doit d’être de. la forme : « x = un nombre… ». C’est ce nombre-résultat, à droite de l'égalité, qui est jugé « bon » ou « faux ». La conséquence, souvent ignorée ou mésestimée est que, pour l’élève, le côté droit de l’égalité (la réponse) se doit d’être d’une longueur minimale, la longueur nécessaire à l'inscription de cet unique nombre-résultat.
Les apprentissages précédents (*) seraient, à eux seuls, de peu d’intérêt (ils seront acquis facilement en cours de scolarité) s'ils n'offraient pas « l'ouverture », « l'allongement » de la partie droite de l'égalité. Cette « ouverture » est celle de la ligne écrite, une opportunité, une occasion à saisir…

Notre élève est préparé à ce type de question. Il vérifie vite que seul un appui sur la touche « 6 » déclenchera un nouvel affichage... et un nouvel allongement de la ligne écrite.…
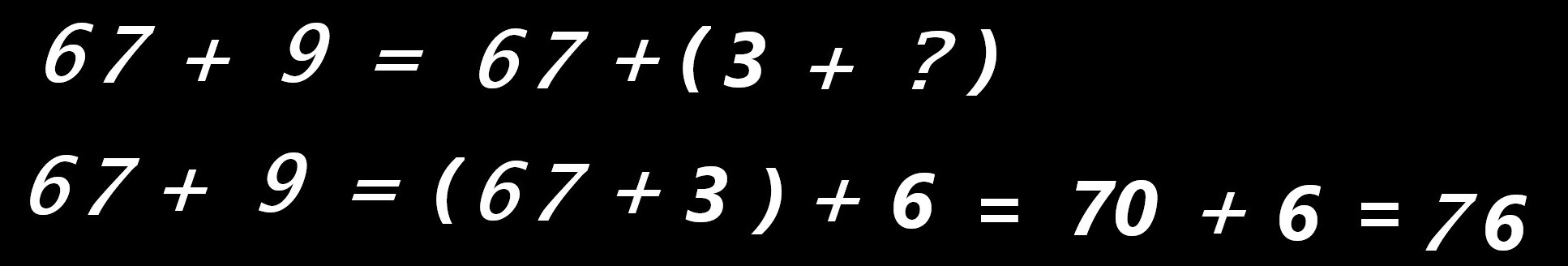
L'écran se fige... quelques secondes... favorisant ainsi une lecture attentive... avant de proposer....

Un appui sur la touche « O » déclenche une nouvelle demande... puis... (si « bonne » réponse...)

. . . un nouvel affichage . . .
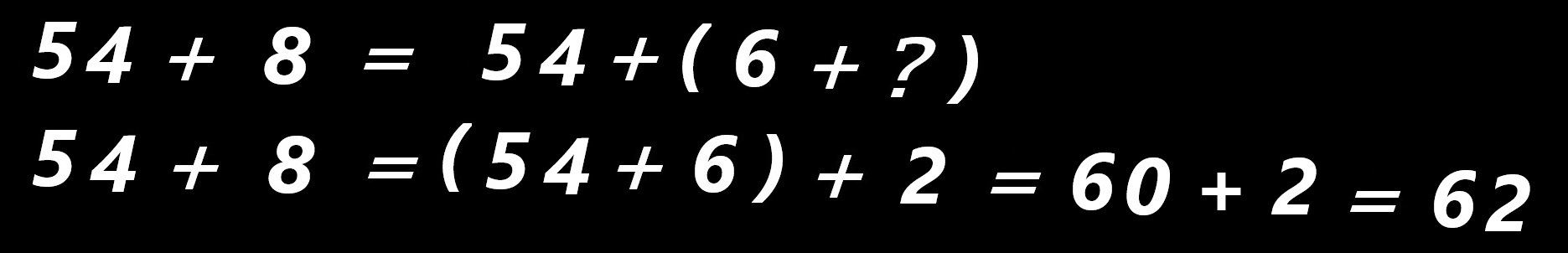
. . . quelques secondes . . (... une lecture attentive...) avant une nouvelle demande....

. . .
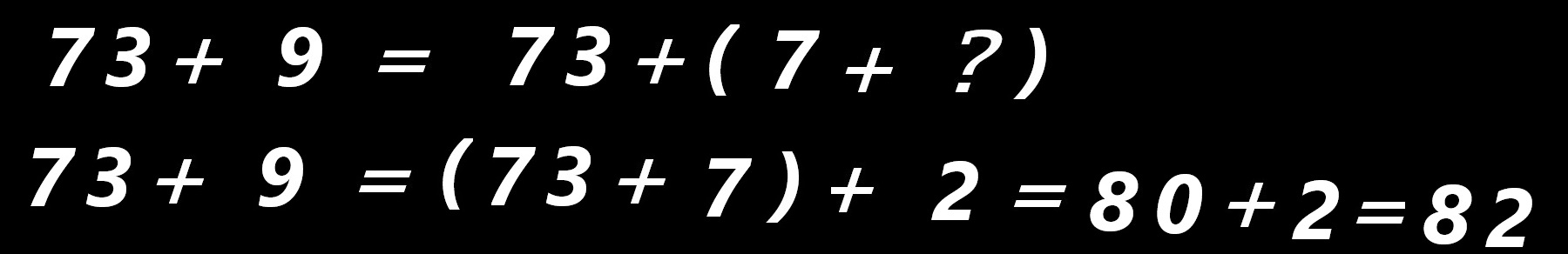
. . .

. . .
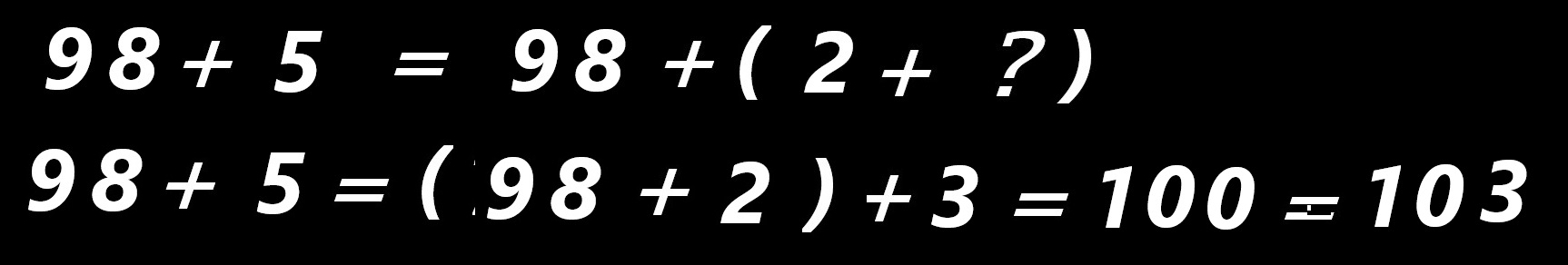
Un appui sur la touche « N » (*) , par contre, déclenche l'apparition d'une image importante, destinée à devenir prépondérante, celle d'une balance en équilibre…

Oublié « le calcul », oubliées « les opérations » : c'est l’imaginaire de l’égalité qui est en cause..
Trois poids (10g, 2g et 5g) sont posés dans le plateau de gauche. On peut évidemment envisager d'autres dispositions sans, pour autant, changer l'èquilibre des deux plateaux :



C’est cette liberté de disposition que traduit et exprime ci-dessous le signe des parenthèses.

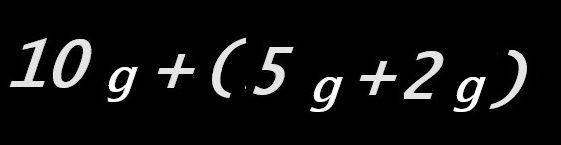
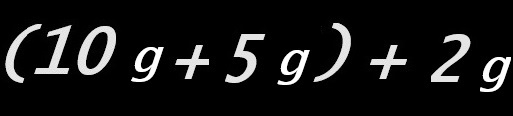
5g et 2g (cinq grammes et deux grammes) sont associées pour « former » 7g (sept grammes). De même, 10g et 5g (dix grammes et cinq grammes), associées, « forment », 15g (quinze grammes).

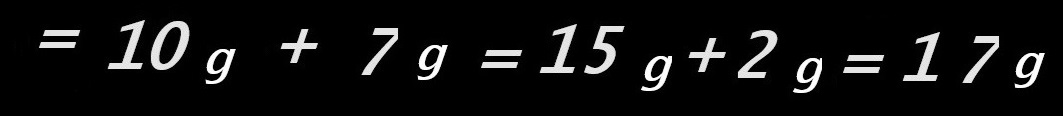
Face à ces images, l’élève, peu à peu prend conscience d'une réalité « algébrique » et...


... du rôle et de l'efficacité de l'écrit dans l'expression (la traduction) de cette réalité.
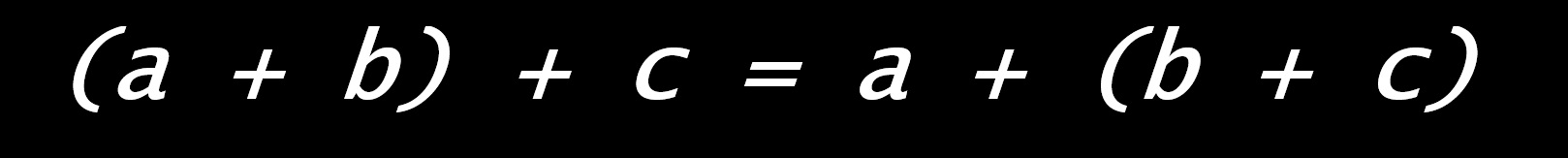
Une fois « associés », les deux termes d’une somme peuvent être « commutés » :


Apprendre à utiliser les parenthèses, à dissocier, commuter puis à réassocier les termes de l'addition. L'élève n'est plus « dans le calcul » ; il raisonne et cela doit se marquer dans ses productions...
Quelques mots très simples y suffisent...