Egalité et similitude
« En » mathématique, ce qui est très particulier et qui impressionne et rebute souvent les élèves (actuels ou anciens) est une exigence : chaque phrase d'un texte mathématique est une affirmation et chaque affirmation doit être considérée comme « vraie ».
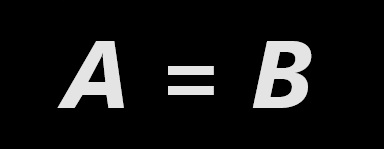
A = B est une phrase et une affirmation : ... A et B « c’est pareil »... c’est « la même « chose » .
C'est cette « chose » qui est «l'objet » mathématique. A et B sont des noms différents de cet objet.
. . .

L’enchevêtrement irréductible du Réel, de l’Image et du Langage est à l’œuvre. Notre élève poursuit sa progression (*). Il est l'auteur de la rédaction ci-dessus. Il a (donc) « neutralisé deux termes opposés », deux « entiers relatifs » et écrit que : « [...] « 67 + 58 », « 70 - 3 + 55 + 3 », « 70 + 30 + 25 », « 125 » [...] » sont quatre noms différents du même nombre, mais je ne pense pas qu'il se soucie beaucoup de ce vocabulaire. Pour lui, l'image de « + 3 et - 3 » a changé : Henri Lebesgue la aussi, là encore...
En passant, je fais remarquer que si l’on définit les opérations sur les nombres positifs et négatifs [...] en remplaçant l’emploi des segments non dirigés par l’emploi des vecteurs, les règles relatives aux signes perdent tout caractère artificiel. (Henri Lebesgue, Sur la mesure des grandeurs, Œuvres scientifiques V, p. 190).
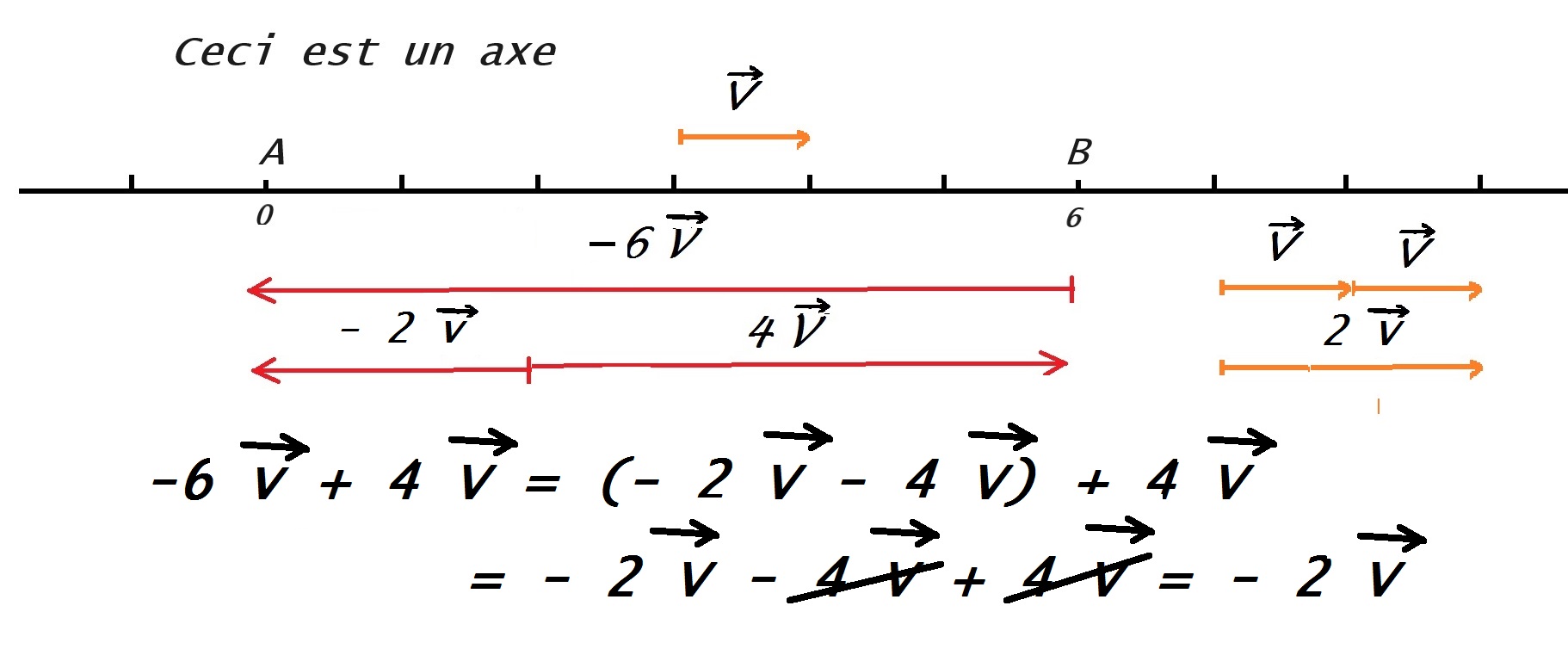
Nombre, longueur, aire, volume, vecteur sont-ils, se distinguent-t-ils...






... comme cinq objets mathématiques à reconnaitre et à (toujours ?) différencier ?

En réponse... la « réalité » géométrique, de nouvelles images? un nouveau langage...
« [...] La notion de similitude [...] est parmi les plus importantes : la notion de corps pareils, plus ou moins gros, s’est imposée aux hommes aussi primitivement et nécessairement que celle d’égalité
(Henri Lebesgue, Message d'un mathématicien.)
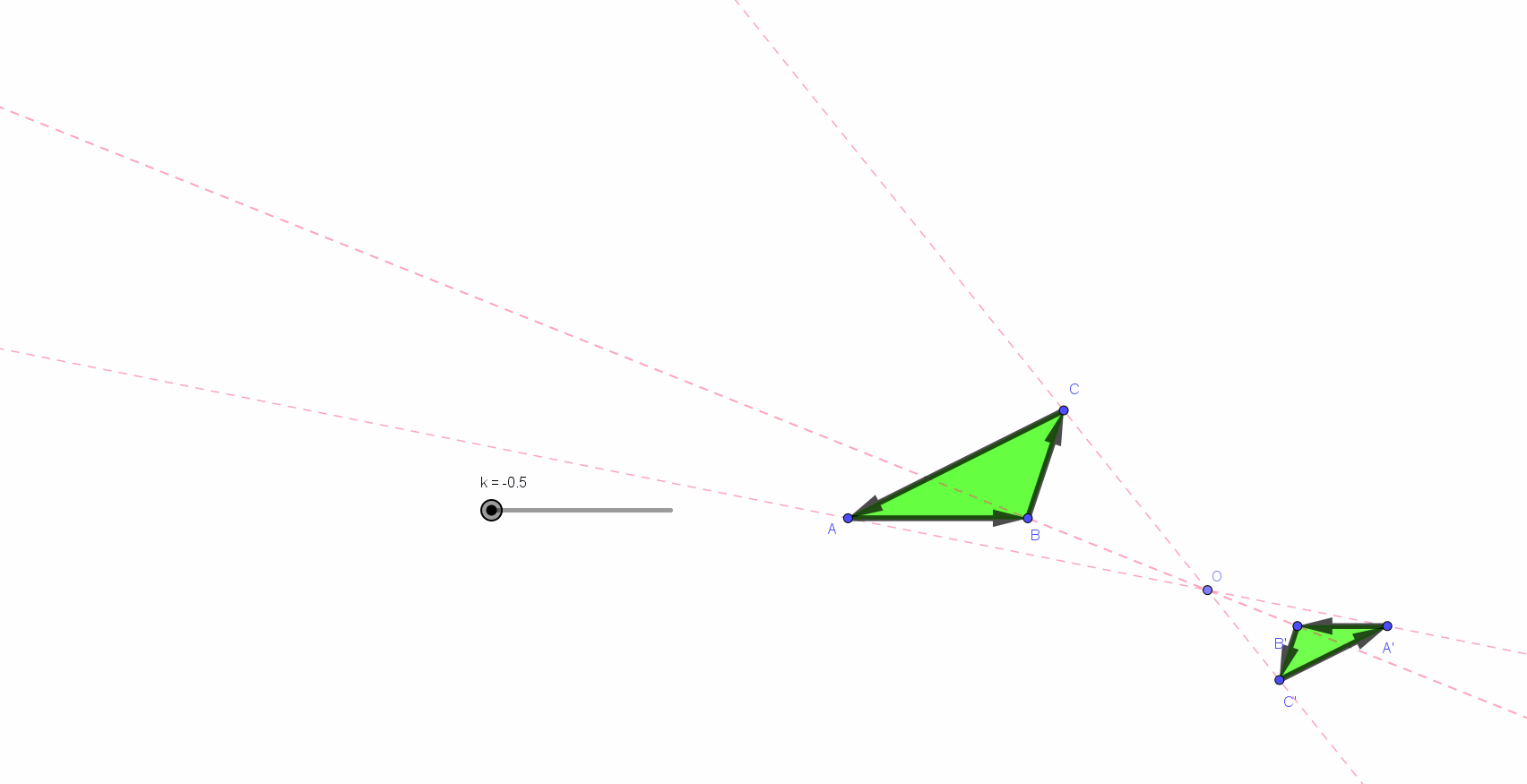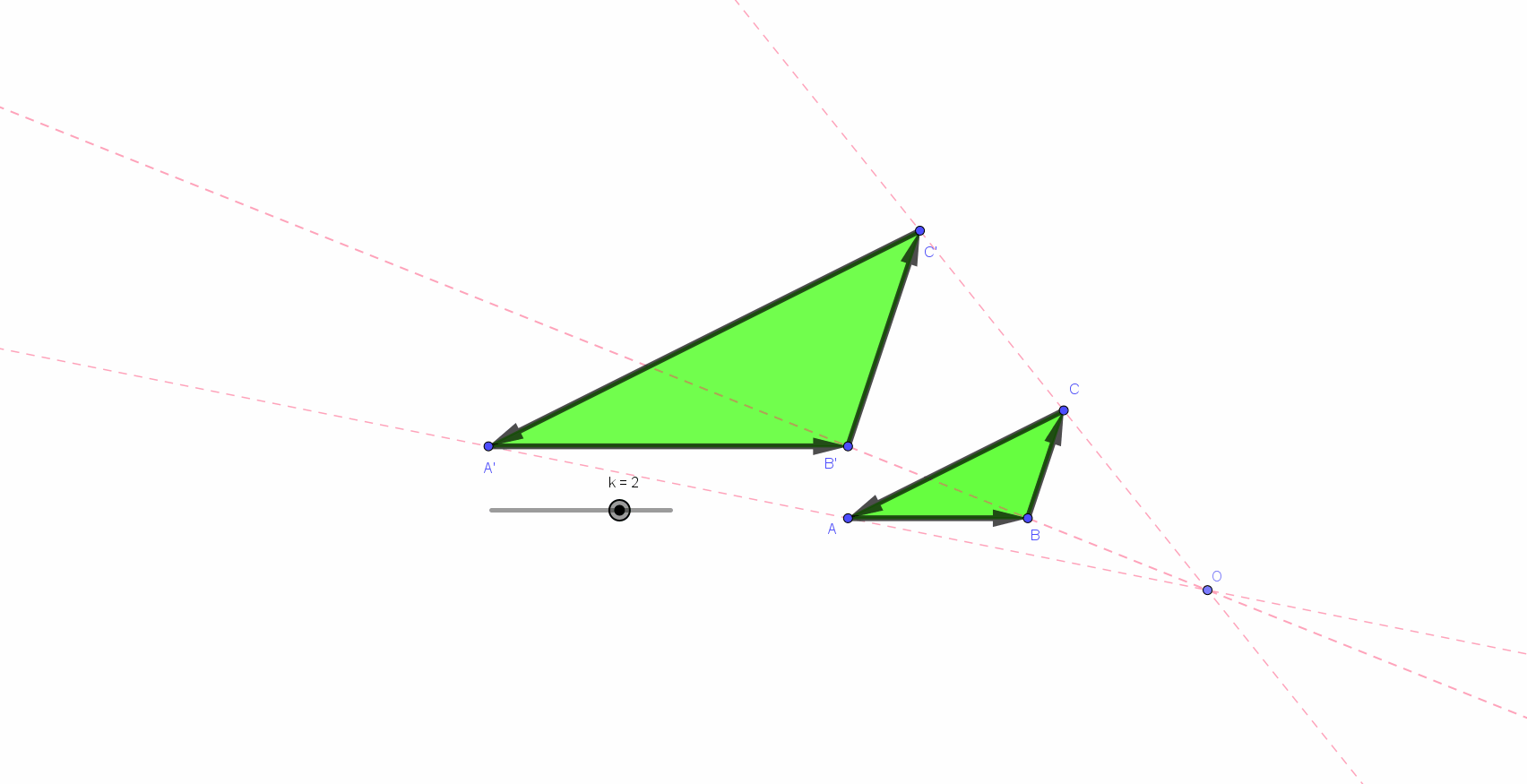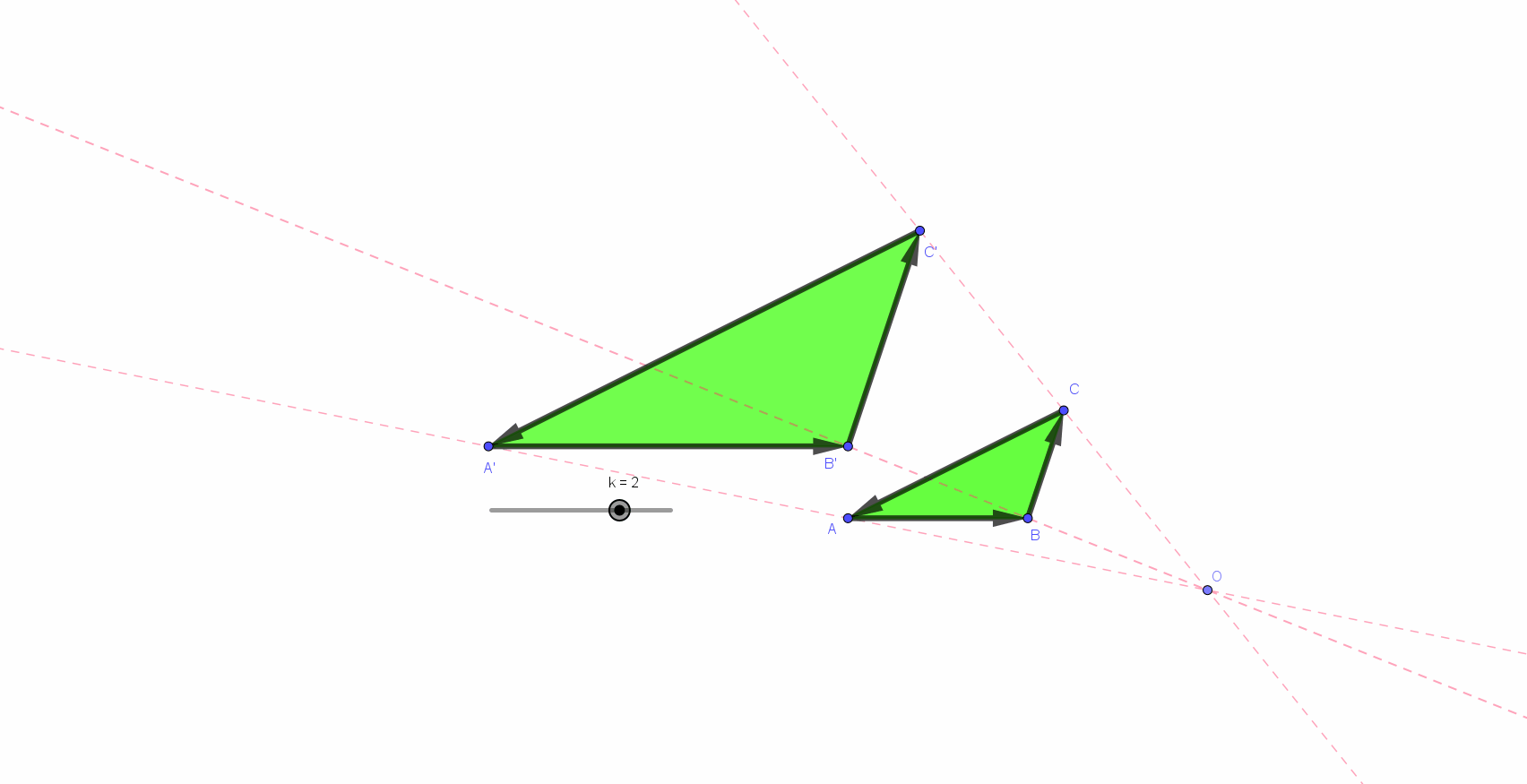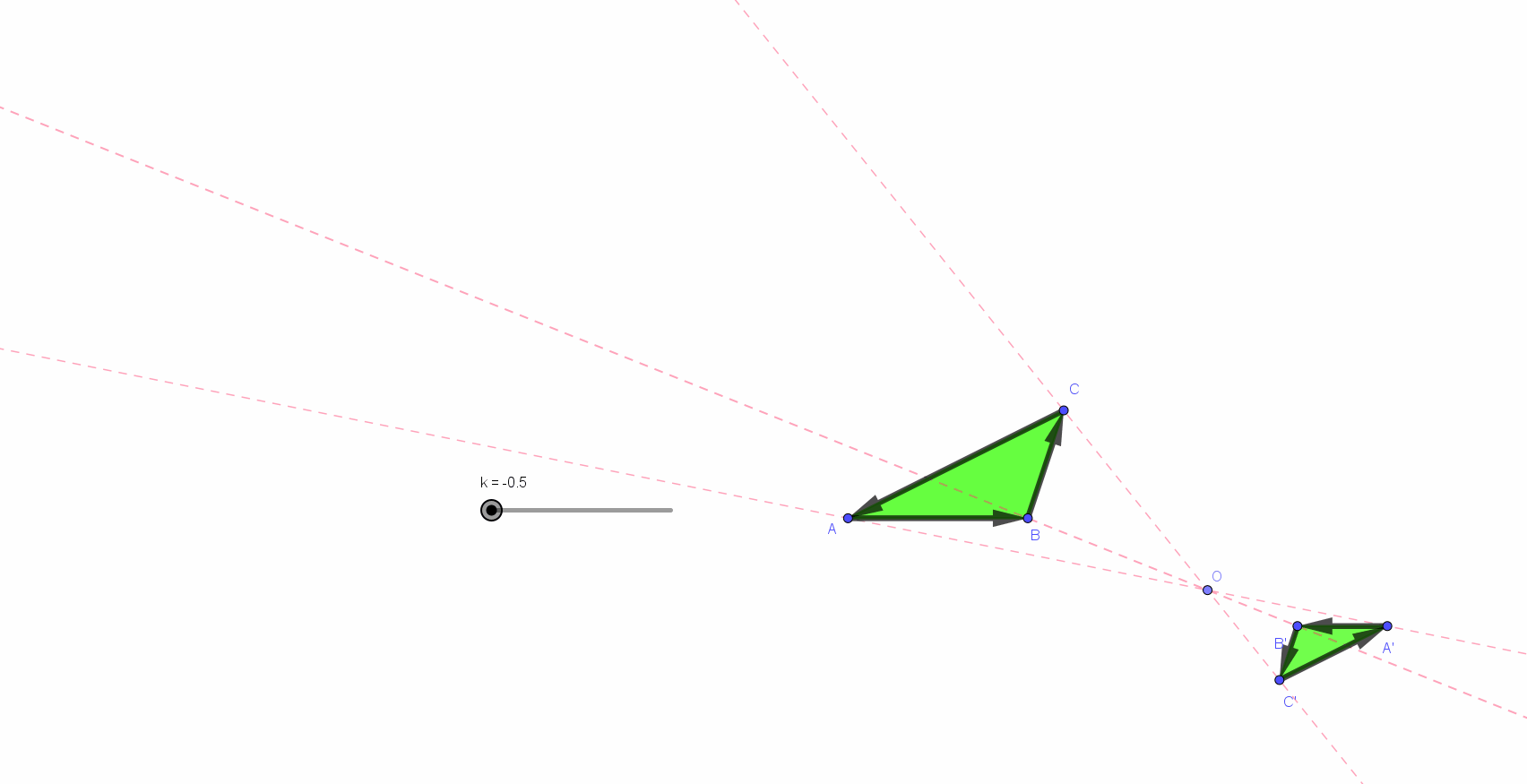
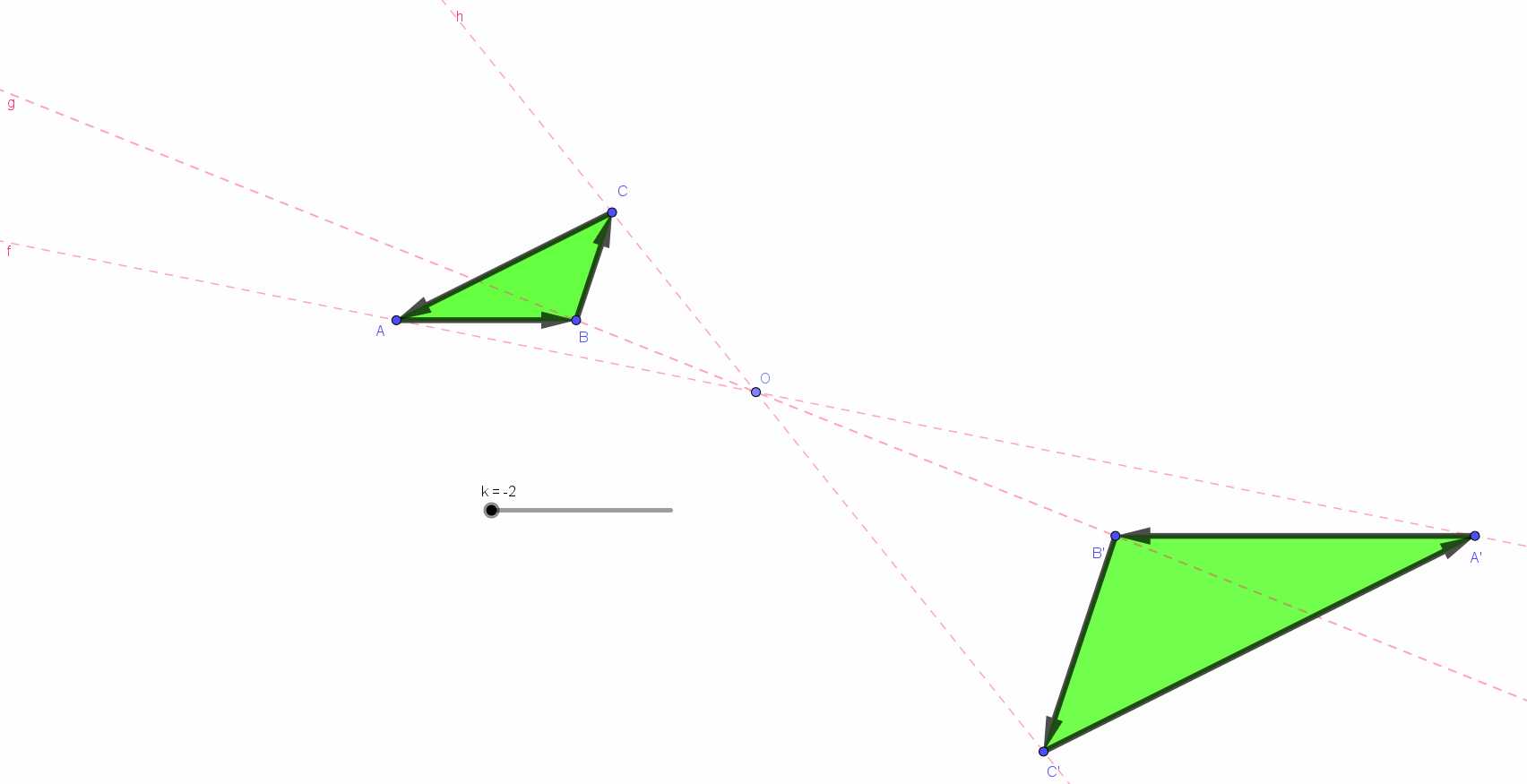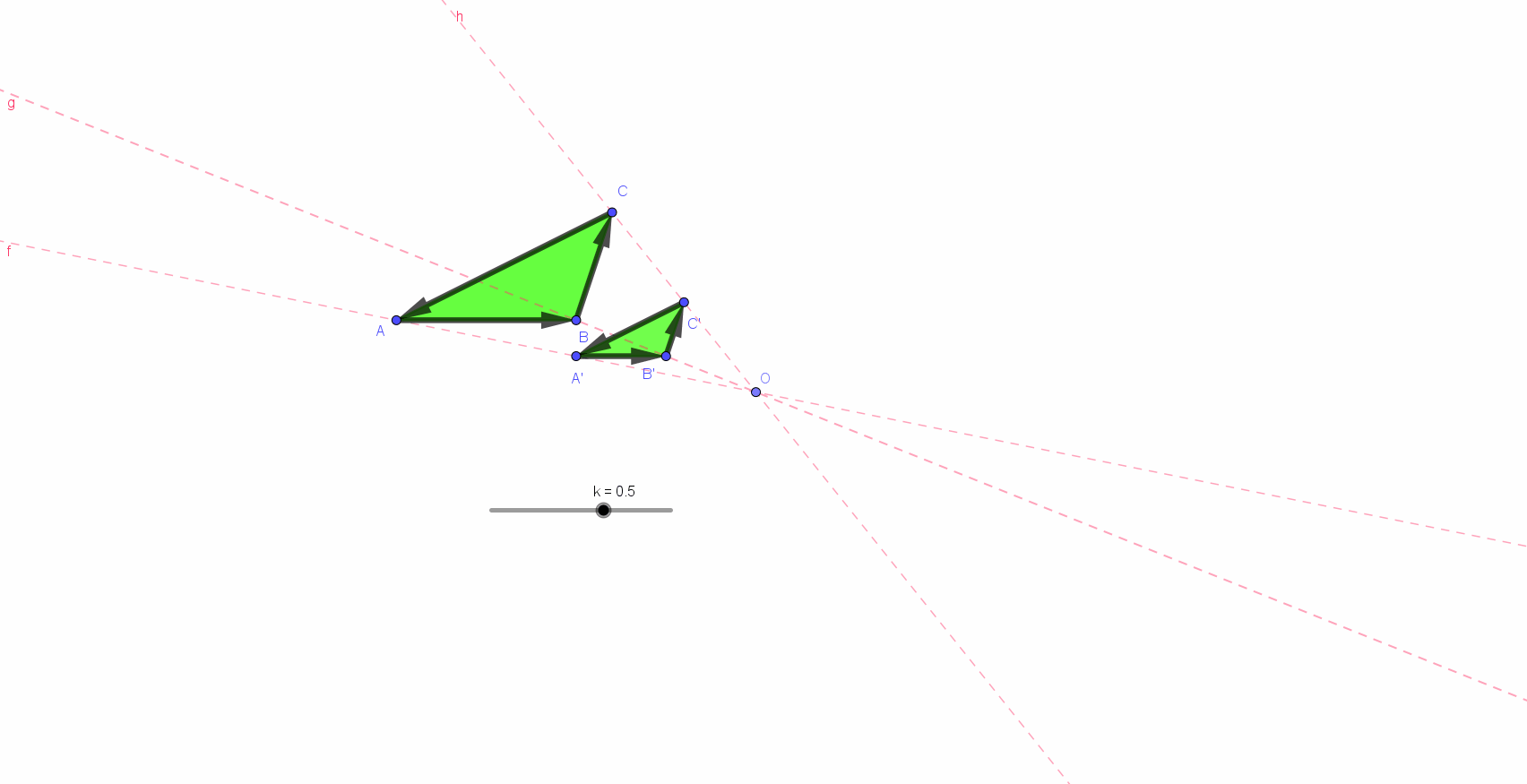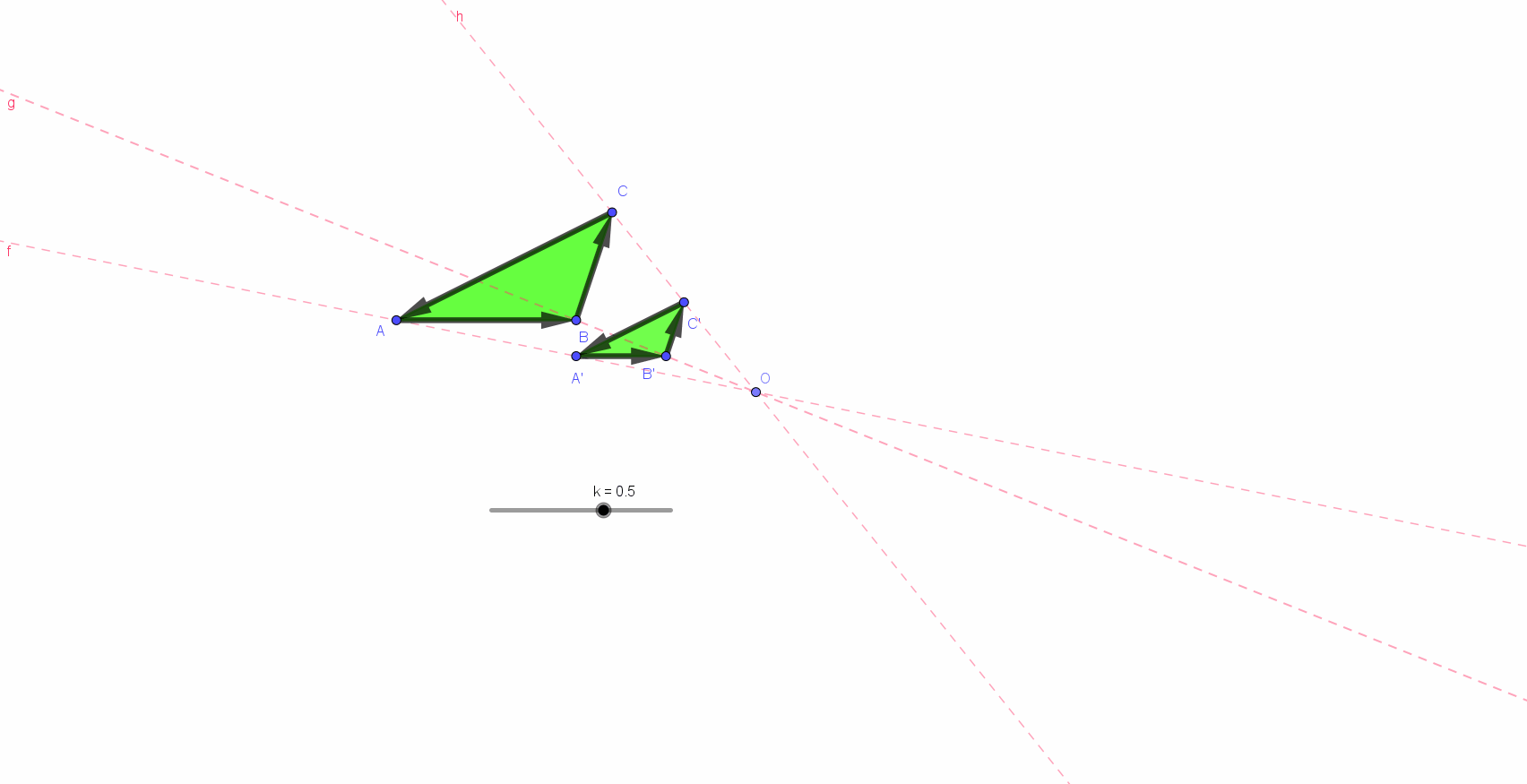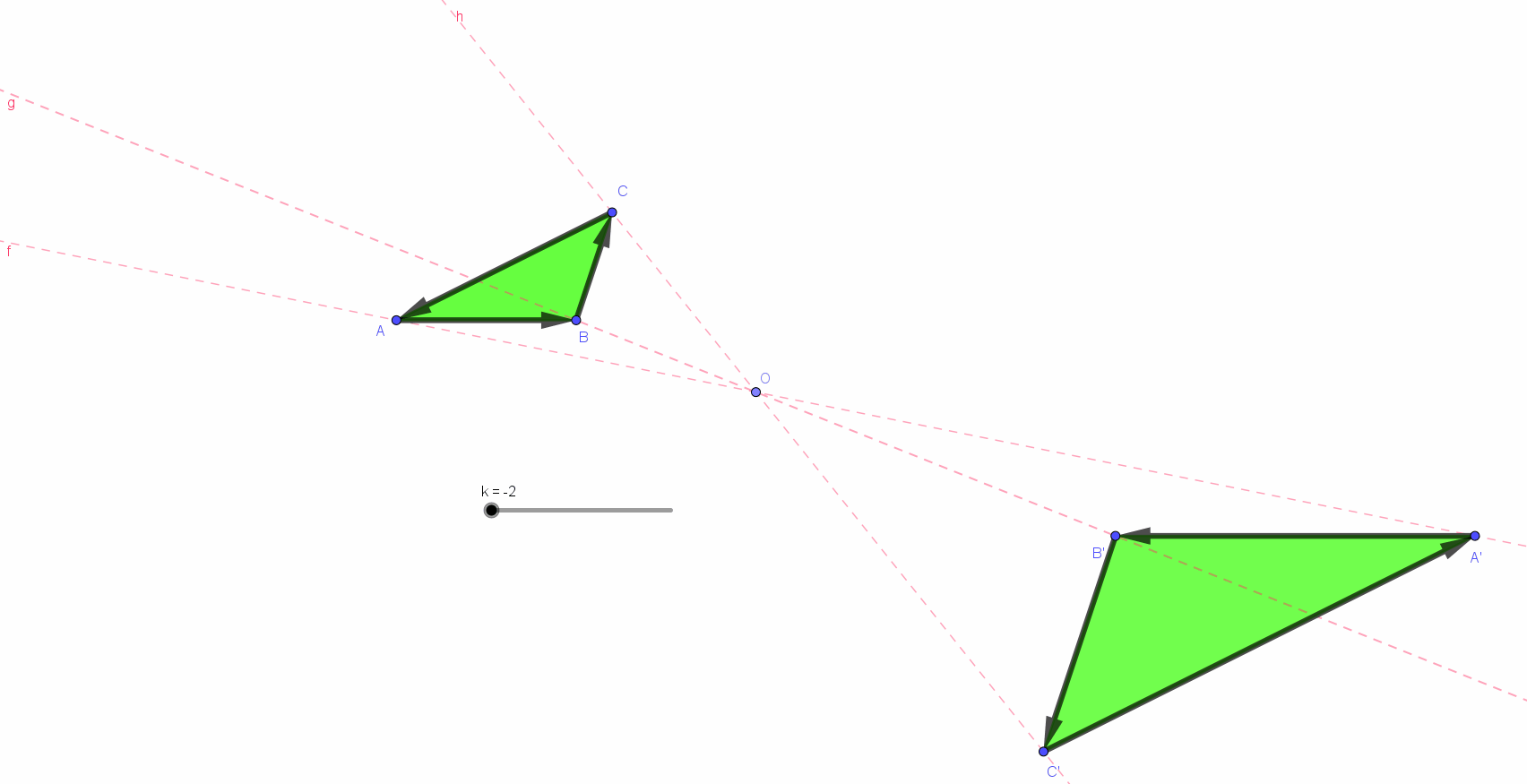
Les deux triangles ci-dessous sont semblables (similaires). Leur similitude est comme résumée, déterminée par un nombre appelé : le rapport de similitude, le rapport de leurs grandeurs (*)).
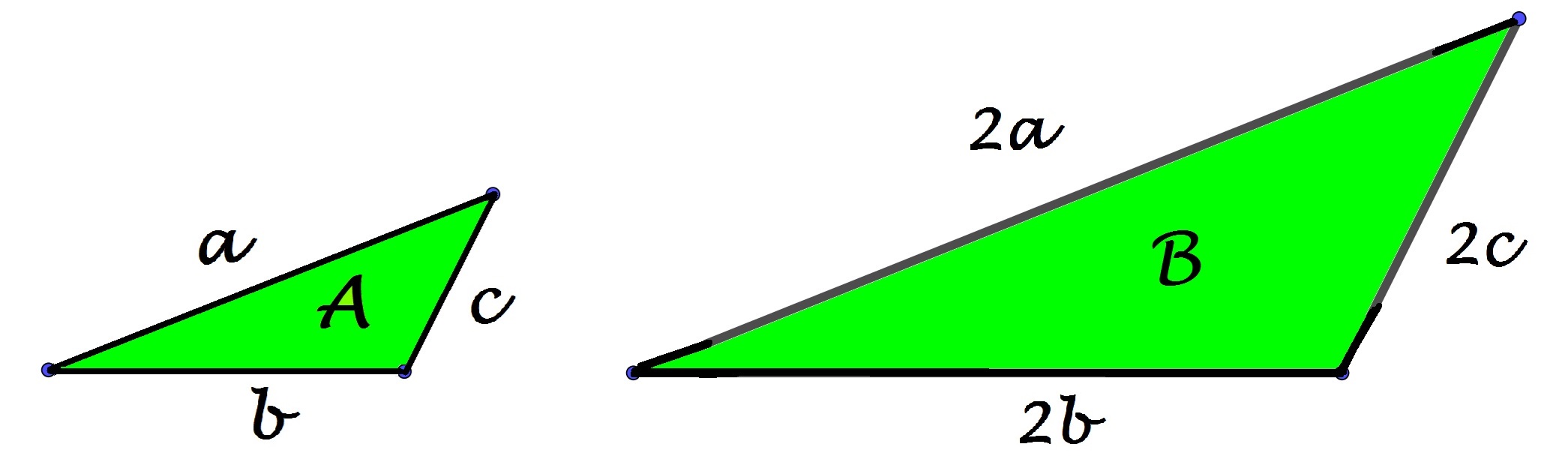
Ce rapport était comme sous-entendu par les notations : les allers-retours du regard (a ➔ 2a, b ➔ 2b et c ➔ 2c) semblent, à eux seuls déterminants. il est de un à deux pour les longueurs. a, 2a, b, 2b, c et 2c sont des longueurs. 2a est (se lit...) le double de a...
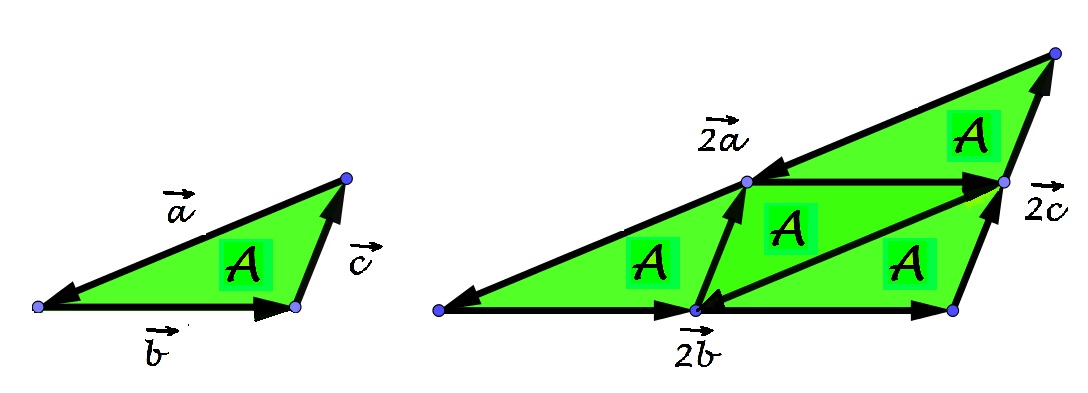
Pour les aires... les lecteurs/spectateurs/auditeurs de la page précédente (*) ont compris et mémorisé ce qu’est l’homothétie. Ils sauront aussi reconnaitre la similitude des triangles ci-dessus et, ainsi, prendre conscience la longueur des côtés et du rapport de cette similitude a, 2a, b, 2b, c et 2c sont des longueurs. 2a est (se lit...) le double de a... Mais quel sens faut-il donner aux « objets » A et B ? La réponse se lit par quelques autres aller-retours du regard : B désigne l"aire du triangle de droite. Cette aire, B, est ... un... deux... trois... quatre fois plus grande que celle, A, du triangle de gauche.
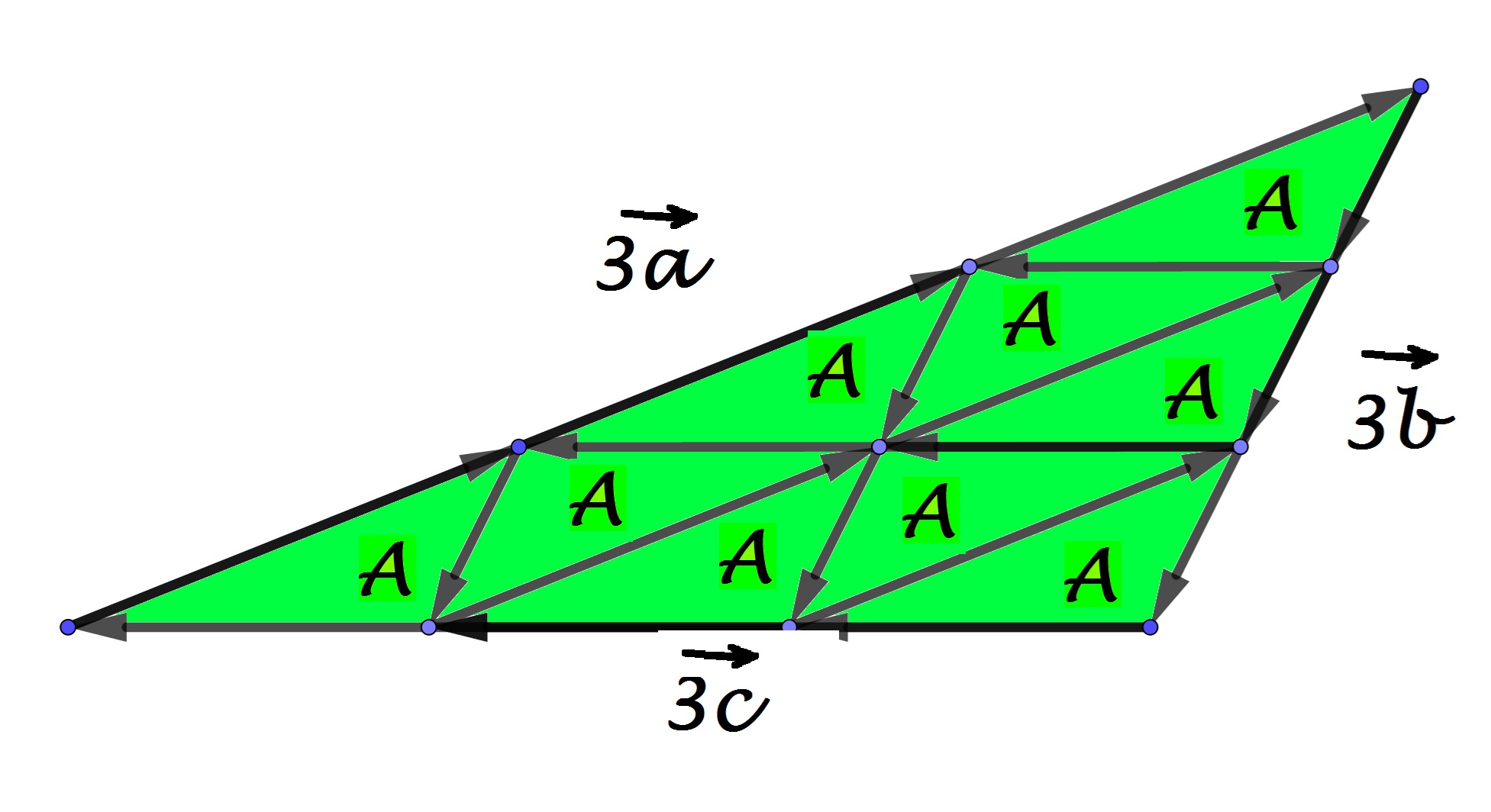
Le décompte est tout aussi « lisible » ci-dessus : l"aire du triangle est ... cinq, plus trois, plus un... neuf fois plus grande que celle du « petit » triangle tout au dessus à gauche. Du triangle « moyen » à ce « grand » triangle, les rapports des longueurs et des aires se « lisent » tout aussi facilement : de deux à trois pour les longueurs et de quatre à neuf pour les aires.

« [...] La notion de similitude [...] est parmi les plus importantes : la notion de corps pareils, plus ou moins gros, s’est imposée aux hommes aussi primitivement et nécessairement que celle d’égalité
(Henri Lebesgue, Message d'un mathématicien.)
« […] La notion importante est celle de figures semblables : l’homothétie n’est que le moyen d’obtenir des figures semblables […] » (Henri Lebesgue, Message d'un mathématicien.)