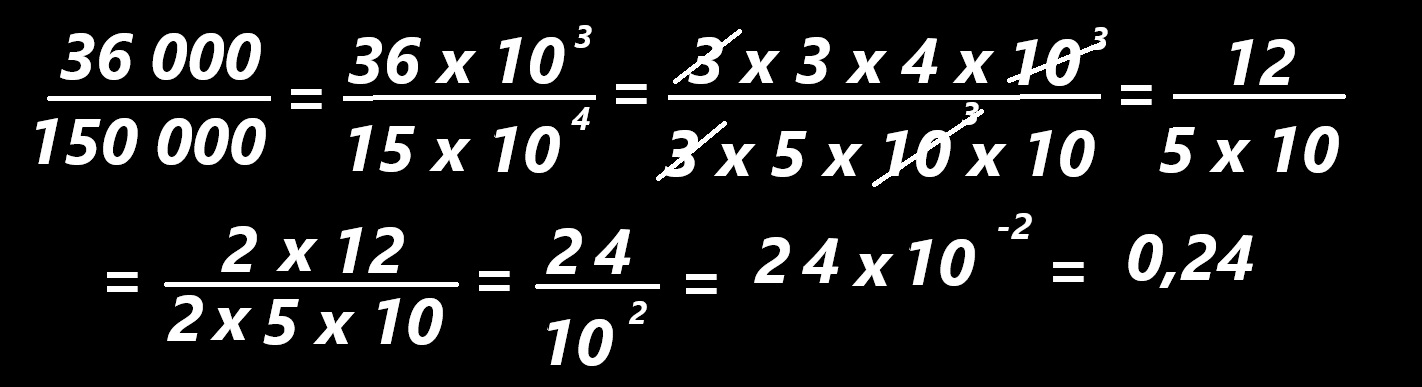
Le monde écolier et ses contraintes
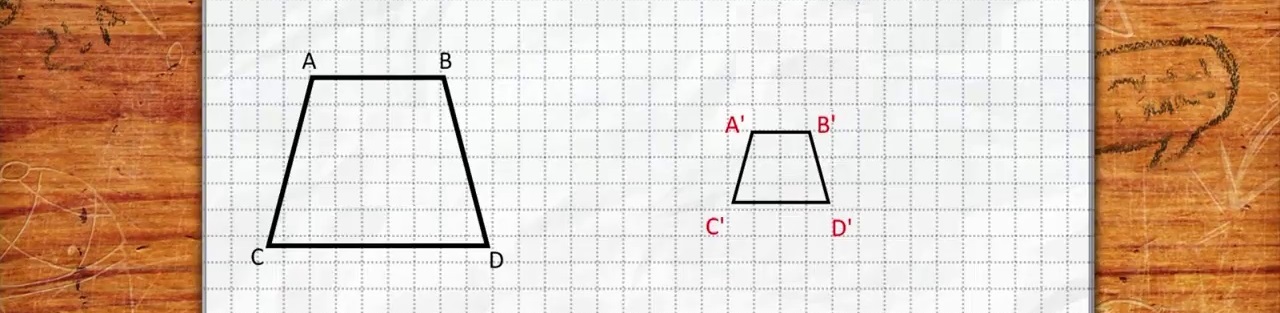
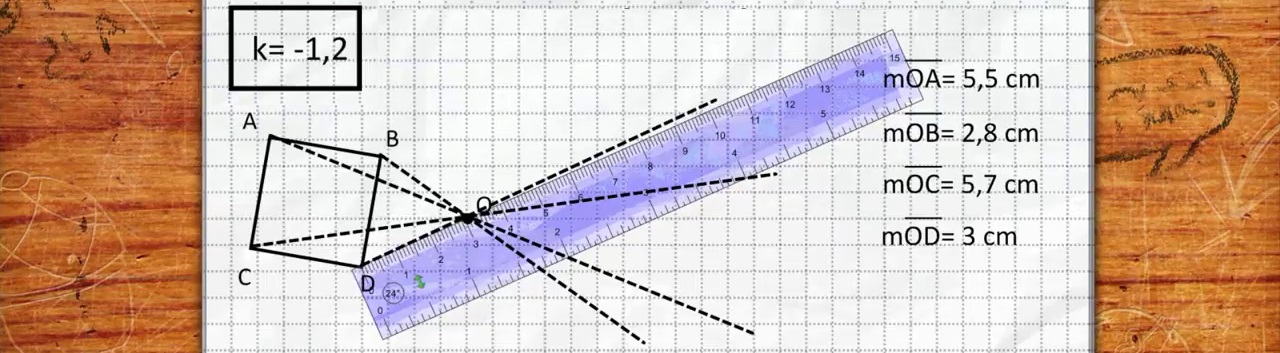
Si vous avez eu la curiosité de regarder et d’écouter quelques minutes de la séquence d'« Alloprof » (*) proposée ci-dessus, vous savez que le langage, le français employé, est celui du Québec. L'imagerie, la mise en scène est celle de l'univers écolier : sa table de travail, la feuille sur laquelle il dessine son univers géométrique, une règle graduée... Les grandeurs mises en rapport sont des longueurs mesurées en centimètres : elles déterminent le réel habituel, quotidien de l'univers écolier.

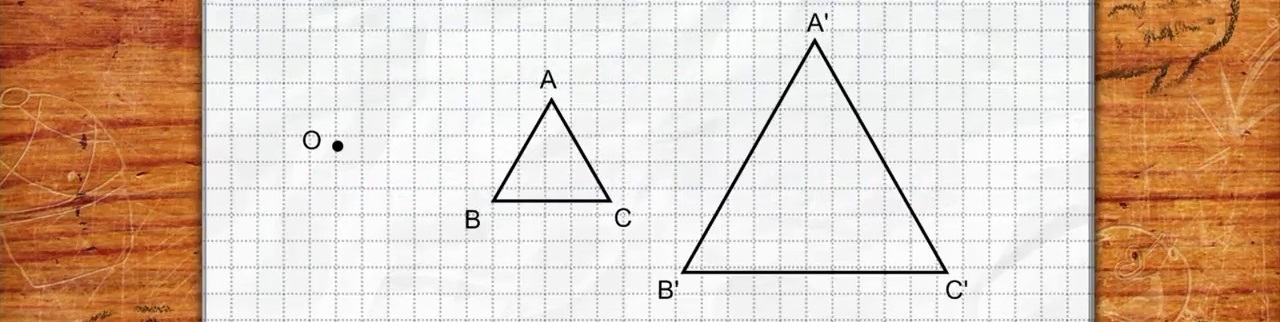
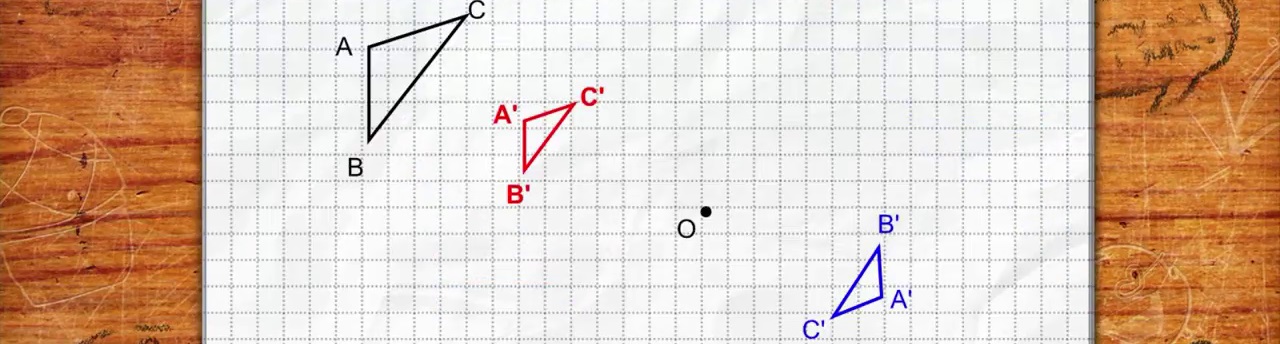
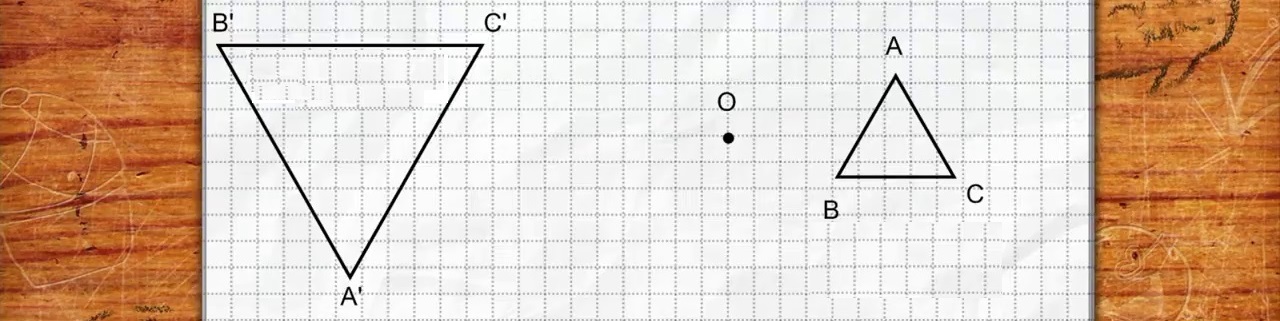
Les animations Géogébra sont elles-aussi soumises aux dimensions des écrans où elles s'affichent.
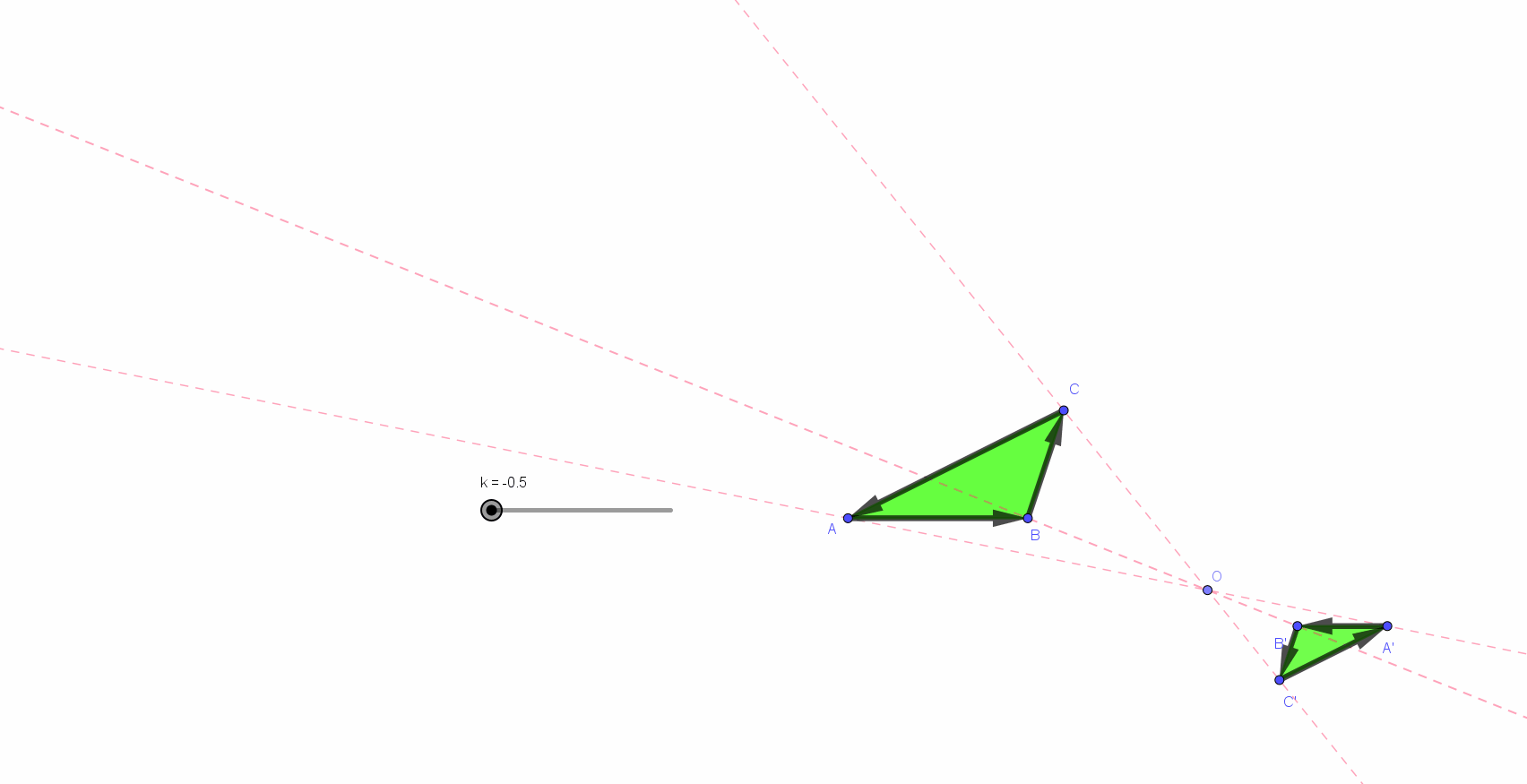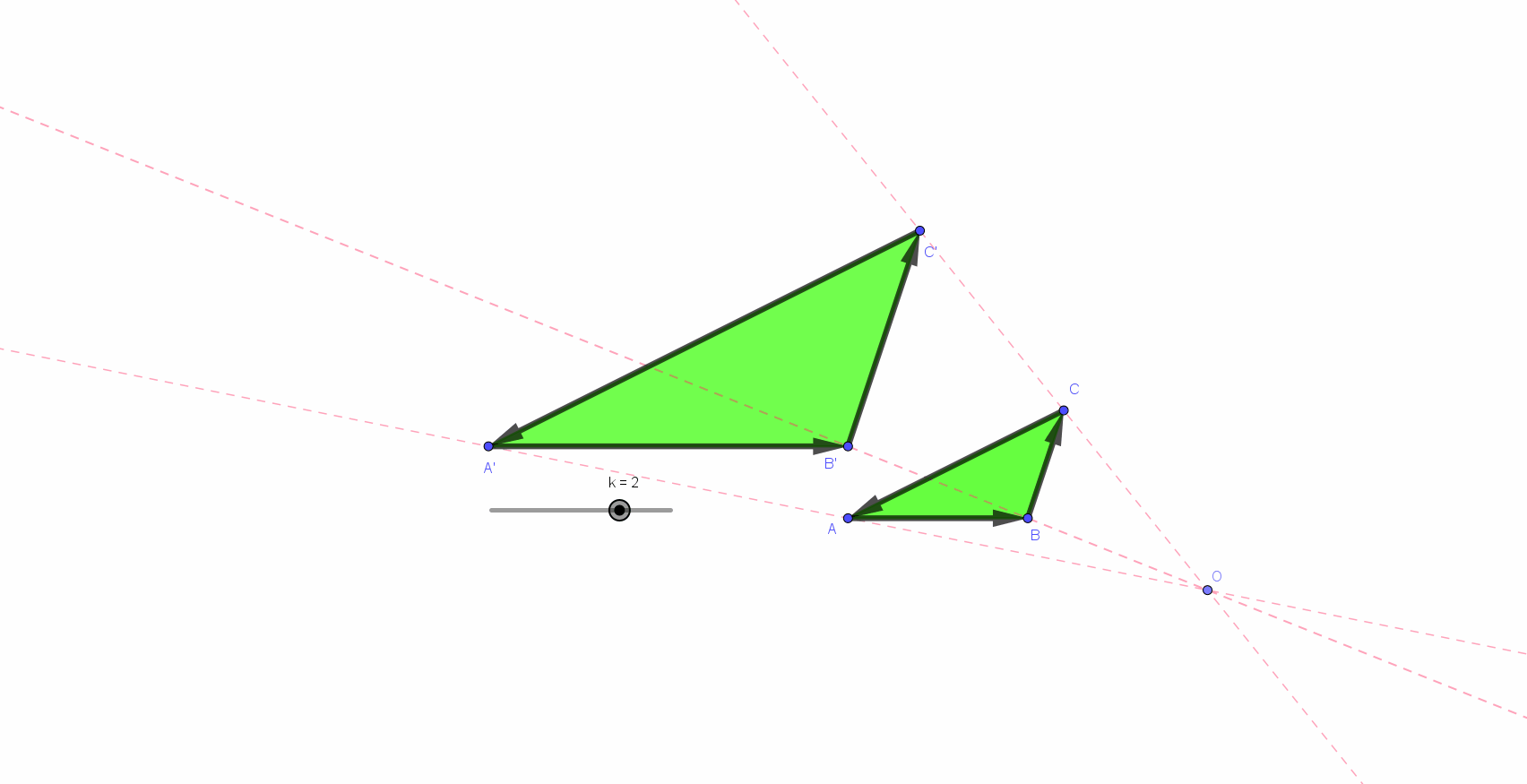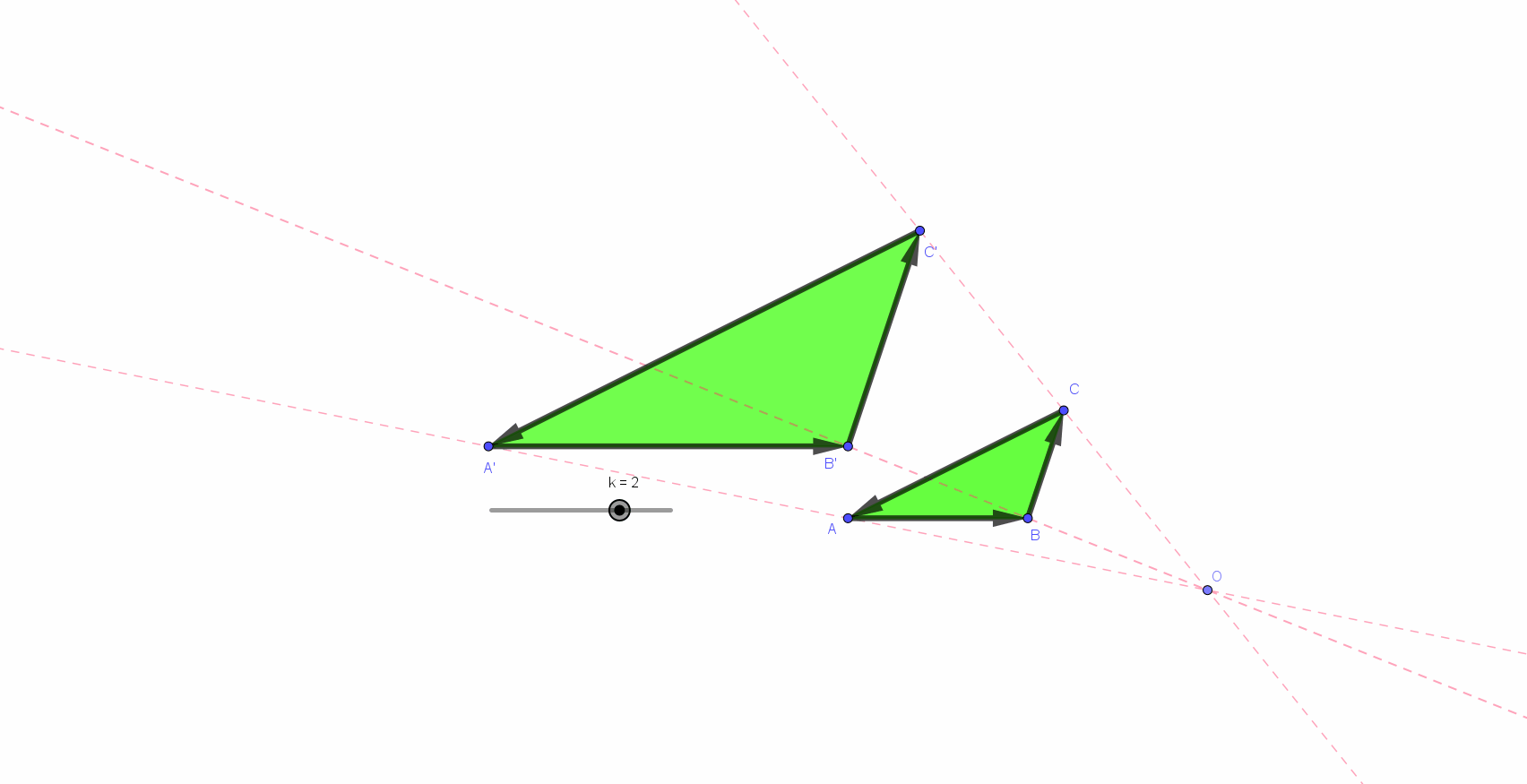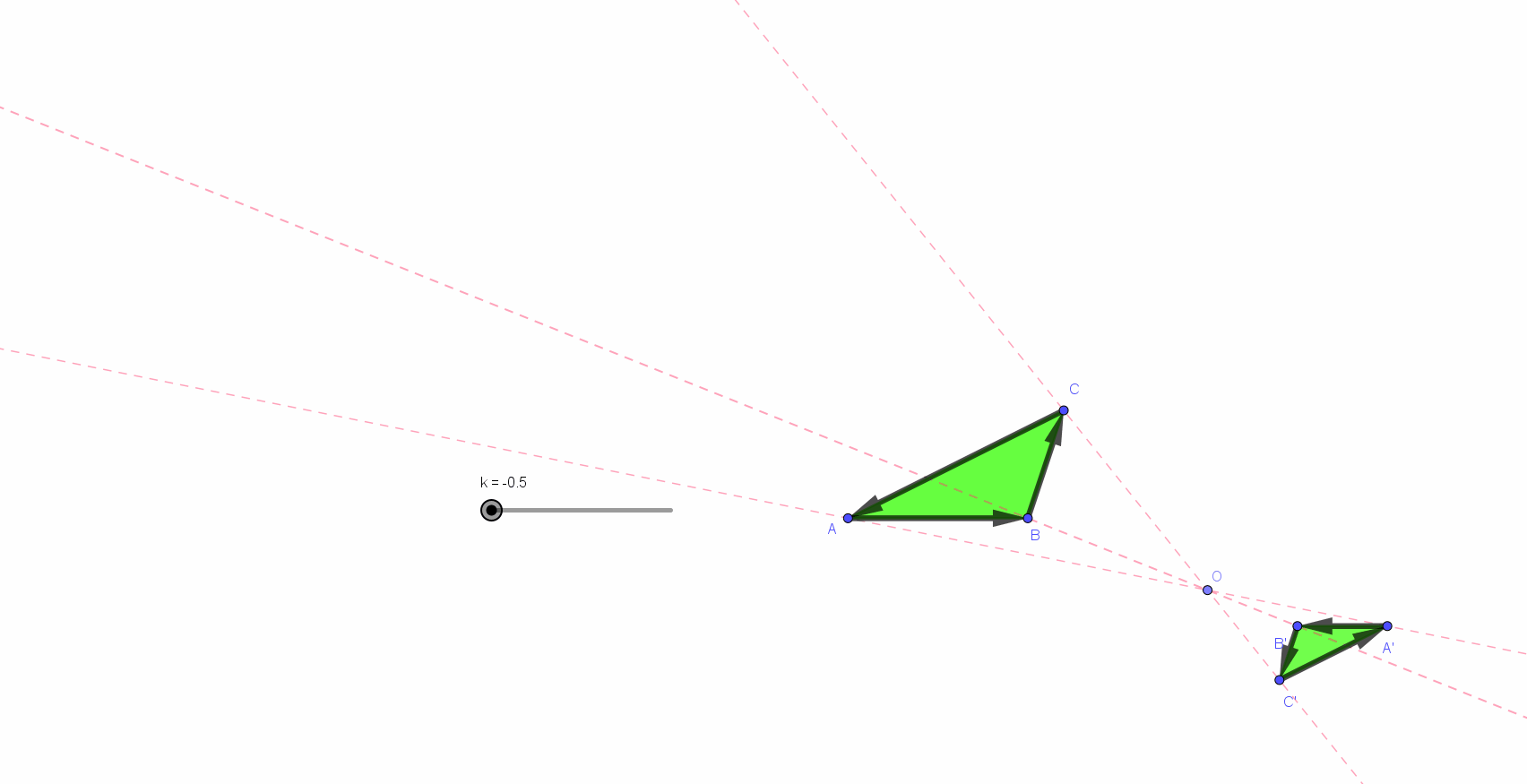
Une évidence : les grandeurs et les rapports de grandeurs pratiqués le plus habituellement dans le monde scolaire sont limités. La simple nécessité de lisibilité et de mémorisation des figures réalisées ou proposées impose des valeurs proches de celles rencontrées et mises en évidence par les représentations « vectorielles » : de un à trois pour les longueurs (et donc) de un à neuf pour les aires (*) .
Le réel, le monde réel, ses contraintes… Élève ou non, sommes-nous préparés à l’affronter ?
Un monde sans fin ?
Élève ou non, nous sommes confrontés au même problème : la taille, la grandeur de la terre...
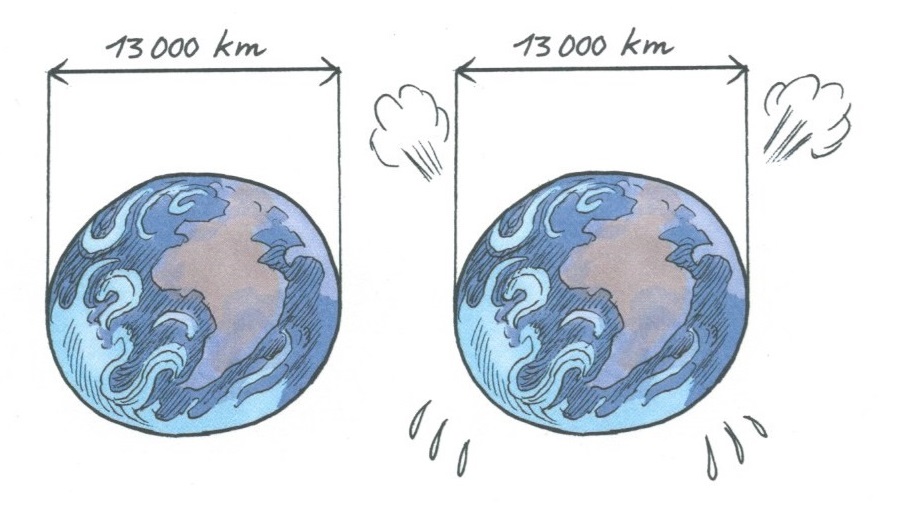
... ne change pas. Par contre, sur sa surface, la taille, la grandeur de la population humaine, son évolution, sa croissance au cours des deux cents dernières années est très inquiétante.

Le pouvoir évocateur d’un récit graphique est impressionnant.. J’espère que Jean-Marc Jancovici et Christophe Blain me pardonneront les copiés-volés ci-dessus (et ci-après) et qu'ils ne verront dans tous ces « emprunts » qu'un hommage (parmi bien d'autres) à leur travail « Le monde sans fin (*). C’est là, dans la connaissance et la conscience des rapports de grandeurs de cette évolution que se situe sans aucun doute l’essentiel des savoirs et des savoir-faire que nous devons tous posséder.
Les publications de l'INED (Institut National d'Etudes Démographiques (ci-dessus)) sont plus précises, plus savantes, mais leur lecture exige un effort particulier, du temps et de l'attention.
Les grandeurs qu'imposent le monde écolier sont bien éloignées de celles des graphiques et des analyses du « Monde sans fin » ou de l'« INED » et nous ne pouvons pas, rapidement et efficacement, modifier ces réalités, ce réel de notre époque. L'élève, notre élève n'est donc pas préparé à comprendre les graves problèmes qu'il devra affronter. Pour les mathématiques élémentaires définies et exposées ici, nous devons choisir et imposer les formes d'un langage mais aussi les images, l'imaginaire qui pourra contribuer aux parises de conscience nécessaires.
« […] Nous avons la chance unique d’avoir à notre disposition une langue universelle, la numération décimale écrite, utilsons-là. […] »
A partir de 600 000 (600 mille), en multipliant par 10 000 (10 mille), on obtient 6 000 000 000, c'est à dire 6 milliards. Au vu et à la lecture de ces nombres, chacun d’entre nous conviendra que « l'opératoire » que veut résumer cet « en multipliant » n'est en fait qu'un simple décompte du nombre de zéros.

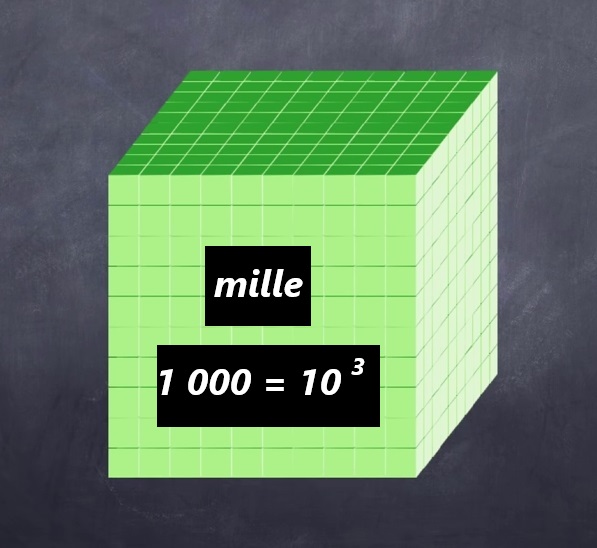
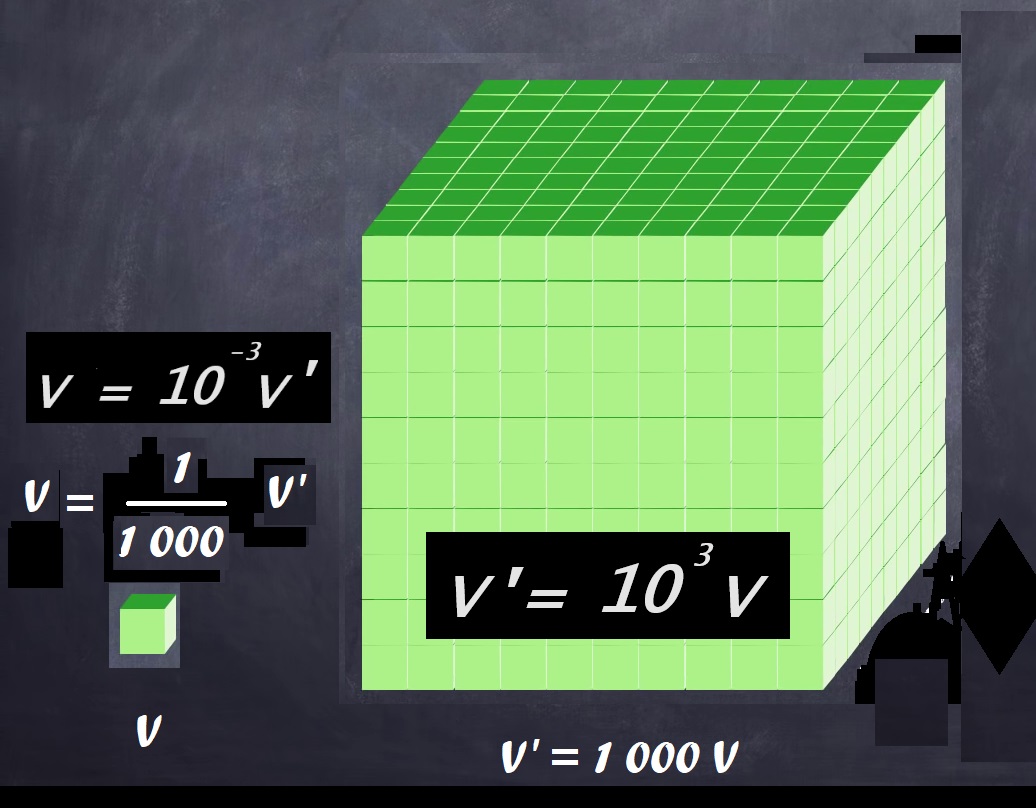
En instituant le « Système métrique », les « Savants de la Révolution » offraient à tous, petits et grands, un moyen simple et pratique de traduire, écrire et effectuer facilement de telles comptabilités. L’idée était simple : différentier les rapports de grandeurs par leurs préfixes : les dixièmes (déci-, 10-1), centièmes (centi-, 10-2)), millièmes (milli-, 10-3) provenaient du latin. Les dizaines (déca-, 101), centaines (hecto-, 102)), milliers (kilo-, 103) étaient des préfixes empruntés au grec.
Au fil des ans, la notation « puissance » imposa sa pratique :
: 600 000 (600 mille) multiplié(s) par 10 000 (10 mille) écrits sous la forme : 6.105 × 104 se lisent et se traduisent facilement et comme naturellement : 6.109. Il suffit ensuite de récapituler en écrivant que :
600 000 × 10 000 = 6.105 × 104 = 6.109 = 6 000 000 000 (à lire 6 milliards)...
Quelques années encore... une rencontre... une autre pratique... l'écriture fractionnaire...