
Nombres et grandeurs
Donner vie, mettre en mouvement les mathématiques et leurs « objets » : voir le trait vertical, ce simple bâton de toutes les comptabilités, prendre vie, se déplacer, se déployer sur les différents niveaux de l’écran. Voir le symbole « + », le signe de l'addition, rouler...
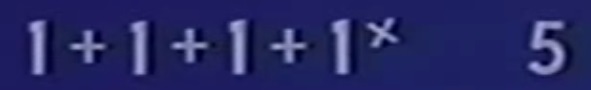
... et ainsi voir (et entendre) se « dérouler » l'arithmétique. A votre gré, dix-neuf secondes (ou plus) : regardez, regardons « Rythmétic ». Pourrons nous « Voir » et même ressentir les difficultés, les soucis du signe de l'égalité...
... bien seul pour vérifier, contrôler dans ce qui se déroule et s'écrit : le sens...

Une fois, deux fois, trois fois, dix fois… plus gros, plus grand, plus long, plus large, plus lourd ?
« [...] Conduire à la notion de volume ! C'est pour nous une notion première ; je veux dire acquise par les enfants avant que nous nous en mêlions. Le bambin qui s'écrie « Mon tas de sable est TROIS FOIS gros comme celui de Renée. » a la notion de volume. [...] » (Henri Lebesgue, Message d'un mathématicien, page 184)
Cette phrase et ce tas de sable nous entrainent dans un univers enfantin : une fois, deux fois, trois fois, dix fois… plus gros, plus grand, plus long, plus large, plus lourd…

On imagine l’enfant, le seau, la « petite » pelle… Henri Lebesgue parle de la notion de volume comme d'une notion première : ce « trois fois plus gros » de l’enfant nous apparait alors comme l’expression de sa fierté. Cette expression mesure « bien des choses » : le volume bien sûr, son évidence, son immédiate visibilité, mais aussi, comme en arrière-plan, le travail, les déplacements, les charges, les transports effectués. Le nombre ne se réalise et ne s'imagine que par la grandeur, la quantité de...

« [...] La notion de similitude [...] est parmi les plus importantes : la notion de corps pareils, plus ou moins gros, s’est imposée aux hommes aussi primitivement et nécessairement que celle d’égalité
(Henri Lebesgue, Message d'un mathématicien... )
Le grand, le moyen et le petit
Enfant ou adulte, comment séparer, coomment extraire de la réalité, du réel ou de l’imaginaire, ce q0ue le langage distingue en nombre et quantité, nombre et grandeurs ? Là encore, les « messages » d’Henri Lebesgue sont essentiels. Trois citations définissent notre programme : (Henri Lebesgue, A propos de la mesure des grandeurs, Œuvres scientifiques volume V, page 190).
« […] La mesure des grandeurs engendre les nombres ; elle n'utilise pas des nombres antérieurement définis de façon abstraite […] »
« […] Notre enseignement n’utilise pas encore pleinement ce fait historique, le plus important peut-être de l’histoire des sciences : l’invention de la numération décimale. […] »
« […] Nous avons la chance unique d’avoir à notre disposition une langue universelle, la numération décimale écrite, utilsons-là. […] »
La notion de volume et la numération décimale… Vingt-cinq secondes ! Qu’en dites-vous ?
L’image de départ est connue et facilement reconnue : une forme, celle d'un cube, un petit cube…
Des lettres apparaissent, des mots se forment, s’alignent : une phrase s’installe, s’impose...

Ensuite...
Une fois…, dix fois…, cent fois…, mille fois…, plus gros, plus grand, plus long, plus large, plus haut ?

Dans un décimètre-cube... « Dans » est un adverbe de lieu. Ce lieu, ce décimètre-cube dans lequel seront placés, rangés mille centimètres-cubes... Le décimètre-cube « volume » devient un décimètre-cube « capacité », capacité à retenir, à enfermer… Du matériel, un jeu d'enfant, une prise en main et des exercices de manipulation s'imposent...



Pour un enfant comme pour un adulte, saisir d'une seule main un cube de un décimètre de côté est difficile à réaliser et surtout à assurer. D'autres formes de récipients de même volume, de même capacité doivent être disponibles et proposées à l'usage. Le litre, le liquide... Pour les liquides, le décimètre cube devient le litre.Les notions de densité (*) et de poids s'annoncent, s'imposent...

Les centimètres cubes jaunes posés dans le plateau droit de la balance sont réalisés en un plastique assez « léger » et certains modèles sont évidés et « calculés » de façon à ce que leur poids soit de un gramme. Un centimètre-cube pour un gramme... la densité de l'eau, un litre/décimètre-cube d'eau pour un kilograme : le choix des savants de la révolution... (*)