Densité et continuité

Ci-dessus, des images d’une réalité que résume bien le nom de leur producteur : « Le grain des bâtisseurs ». Les techniques exposées répondent à un souci bien réel lui aussi : comment « bâtir », comment construire « du solide » ? Ce grain est-il une réponse à la question posée précédemment (*) celle d’un point matériel ? Ci-dessous des images d’usage, habituelles « en » mathématique :

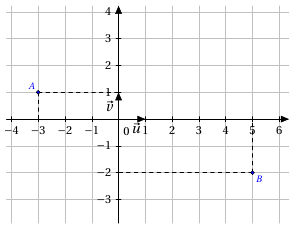
A gauche, l'image de l'armature constitutive du solide; à droite celle du plan réel mathématique.

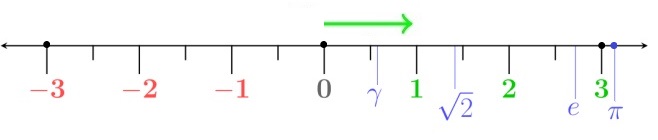
Ci-dessus trois images de ce qui par convention, « en » mathématique, est appelé : droite réelle.

Notre modèle (R.S.I.* *), l’enchevêtrement réel-langage-imaginaire s’affirme avec deux images : celle d'un point/grain (une marque ronde sur la droite) et celle d'un point trait (trait de coupure de la droite). Un soupçon prend forme : celui d’une astuce, d’un jeu sur le langage, d’un jeu de miroir : les mathématiques idéalisent l'image du point pour parler, pour décrire le nombre, lui donner une réalité. Ci-dessus sont rassemblés en un même point de vue, en un même ensemble les nombres appelés réels. Notre élève imaginaire rencontrera vite le nombre « π ». Pourquoi ne pourrait-on pas, alors, à cette occasion, lui donner à voir une suite de chiffres indéfinie vers la droite et comportant une virgule ?

C'est de ce point de vue qu'Henri Lebesgue présente ce qu'il appelle nombre le plus général :

Cette présentation, cette notion de nombre le plus général en impose une autre... pratique...

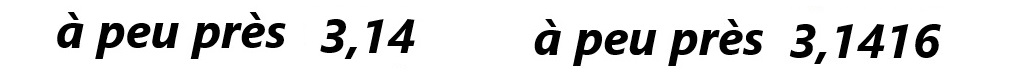
Peut-être avez-vous remarqué ce court passage de « L’homothétie (*) » où il est écrit que :

Ce « 0,70 » provient incontestablement de la division de 3,9 par 5,6. Les « centimètres » n’ont ici d’autre rôle que de rappeler le rapport originel, rapport de deux mesures de lonqueur, compte rendu de deux affirmations : D'C' = 3,9cm et DC = 5,6cm (ces deux égalités ne sont vraies que par hypothèse...).

Lorsque vous « tapez » 3.9 « divisé par » 5,6 sur votre calculatrice s « standard » l’écran affiche :

Sur l’écran d’une calculatrice « scientifique » et avec la même frappe, vous obtienez :

Ce second affichage prolonge le précédent et confirme ce qui semblait déjà une évidence...

... l'apparition d'une série de six chiffres, série répétitive constituante de l'écriture décimale...

Notre élève imaginaire possède les bases de la numération décimale et ce « 0,70 » proposé comme « résultat » d’une division permet d’aborder avec lui la notion de diviseur puis de « diviseur et facteur premier ». Nous sommes ainsi face à ce « nombre le plus général », résultat et compte rendu d’une expérience. Appelons-le un développement décimal illimité périodique et, pour abréger, un d.d.i.p.

Ce « 0,70 », par convention, constitue la valeur approchée au centième près de ce d.d.i.p..

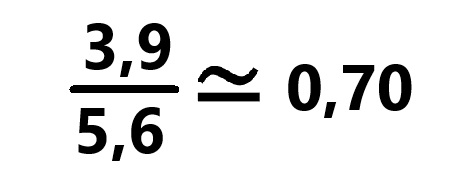
Il suffit de lire attentivement le d.d.i.p. (en rouge ci-dessus) : 0,7 est la valeur approchée au dixième près et 0,70 la valeur approchée au centième près. Ensuite : 0,696 est au millièmee près, 0,6964 au dix-millième près et 0,69643 au cent-millieme près. Dans la « vie réelle », chaque utilisateur d'un d.d.i. ou d'un d.d.i.p. est à même de déterminer et de choisir la précision qui lui est nécessaire.

Parmi toutes ces images, remarquons celle d’une droite, mais d’une droite chargée d’un langage particulier : à chaque pont de cette droite est associé un nombre unique appelé son abscisse. C’est, au sens fort de ce mot, une confusion qui, ainsi, est crée entre points et nombres. L’enchevêtrement du réel, du langage et de l'image autorise (heureusement) quelques astuces : cette droite est ainsi élevée au rang, à la dignité de modèle. Du même mouvement, chaque point est considéré comme réel et, lui aussi, comme un modèle. Le nombre associé à ce point (le représentant de ce point) est appelé nombre réel.

... Densité et continuité...

… Le nombre représente le point... La confusion de deux objets ainsi établie est facilement réversible et se formule alors... le point représente le nombre... C'est alors le modèle qui est en question :

La ligne droite se trace, se montre, apparait comme continue : cette image et ce vocabulaire s'imposent d'eux mêmes. Une question, alors, se pose et s'impose elle aussi : cette continuité peut-elle être applicable aux nombres réels imagés, imaginés, figurés dans leur ensemble ?

Cette question (la continuité des points de la droite « réelle ») va se déplacer, « se transposer » : l’image du point-grain-de-matière disparait, un point-intersection-de-traits s’installe :

L'imagination se reporte alors sur lidée d'un ordre ordre commun aux points et aux nombres :